AUTOMATIC DETECTION OF CHANGES IN THE ENVIRONMENT

Nils Hamel (UNIGE)

Project scheduled in the STDL research roadmap - TASK-DIFF
September 2020 to November 2020 - Published on December 7, 2020

This work by STDL is licensed under CC BY-SA 4.0

Abstract : Developed at EPFL with the collaboration of Cadastre Suisse to handle large scale geographical models of different nature, the STDL 4D platform offers a robust and efficient indexation methodology allowing to manage storage and access to large-scale models. In addition to spatial indexation, the platform also includes time as part of the indexation, allowing any area to be described by models in both spatial and temporal dimensions. In this development project, the notion of model temporal derivative is explored and proof-of-concepts are implemented in the platform. The goal is to demonstrate that, in addition to their formal content, models coming with different temporal versions can be derived along the time dimension to compute difference models. Such proof-of-concept is developed for both point cloud and vectorial models, demonstrating that the indexation formalism of the platform is able to ease considerably the computation of difference models. This research project demonstrates that the time dimension can be fully exploited in order to access the data it holds.

Task Context : Difference Detection

As the implemented indexation formalism is based on equivalences classes defined on space and time, a natural discretization along all the four dimensions is obtained. In the field of difference detection, it allowed implementing simple logical operators on the four-dimensional space. The OR, AND and XOR operators were then implemented allowing the platform to compute, in real time, convolutions to compare models with each others across the time.

The implementation of these operators was simple due to the natural spatio-temporal discretization obtained from the indexation formalism. Nevertheless, two major drawbacks appeared : the first one is that such operators only works for point-based models. Having the opportunity to compute and render differences and similarities between any type of data is not possible with such formal operators.

The second drawback comes from the nature of the point-based capturing devices. Indeed, taking the example of a building, even without any change to its structure, two digitization campaigns can lead to disparities only due to measures sampling. The XOR operator is the natural choice to detect and render differences, but this operator is very sensitive to sampling disparities. Computing the XOR convolution between two point-based models leads the rendering to be dominated by sampling variations rather than the desired structural differences.

This drawback was partially solved by considering the AND operator. Indeed, the AND operator allows to only shows constant structural elements from two different positions in time and is insensitive to sampling disparities. As shown on the following images, the AND operator shows differences as black spots (missing parts) :

AND convolution between two LIDAR models : Geneva 2005 and 2009 - Data : SITG

As one can see, AND convolutions allow detecting, through the black spots, large area of structural changes between the two times and also, with more care, allow guessing smaller differences. Nevertheless, reading and interpreting such representation remains complex for users.

The goal of this task is then to tackle these two drawbacks, allowing the platform to detect changes not only for point-based models but also for vector-based models and to implement a variation of the XOR operator for point-based models allowing to efficiently highlight the structural evolution. The task consists then in the implementation, testing and validation of a difference detection algorithm suitable for any type of model and to conduct a formal analysis on the best rendering techniques.

Methodology

A step by step methodology is defined to address the problem of difference detection in the platform. In a first phase, the algorithm will be developed and validated on vector-based models as follows :

• Obtaining a large scale vector-based model on which synthetic variation are introduced

• Development of the algorithm using the synthetic variations model

• Testing and validation of the algorithm (using the known synthetic variations)

• First conclusion

In a second phase, true land register data will be used to formally detect real evolutions of the territory :

• Obtaining true land register vector-based models (INTERLIS) at different times

• Analysis of the difference detection algorithm on true land register vector-based models

• Second conclusion

In a third phase, the algorithm will be validated and adapted to work on point-based models :

• Obtaining true land register point-based models (LAS) at different position in time

• Verifying the performances of the vector-based detection algorithm on point-based data

• Adaptation of the algorithm for point-based models

• Analysis of the difference detection algorithm on true land register point-based models

• Comparison of the detected differences on point-based models and on their corresponding land register vector-based models (INTERLIS)

• Third conclusion

In addition, the development of difference detection algorithm has to be conducted keeping in mind the possible future evolutions of the platform such as addition of layers (separation of data), implementation of a multi-scale approach of the time dimension and addition of raster data in the platform.

First Phase : Synthetic Variations

In order to implements the vector-based difference detection algorithm, sets of data are considered as base on which synthetic differences are applied to simulate the evolution of the territory. This approach allows focusing on well controlled data to formally benchmark the results of the implemented algorithm. Experiments are conducted using these data to formally evaluate the performance of the developed algorithm.

Selected Resources and Models

Vector Models : Line-based

In this first phase, line-based data are gathered from openstreetmap in order to create simple models used during the implementation and validation of the detection algorithm. A first set of vector-based models are considered made only of lines. Three sets are created each with a different scale, from city to the whole Switzerland.

The line-based sets of data are extracted from openstreetmap shapefiles and the elevations are restored using the SRTM geotiff data. The EGM96-5 geoid model is then used to convert the elevation from MSL to ellipsoid heights. The following images give an illustration of these sets of data :

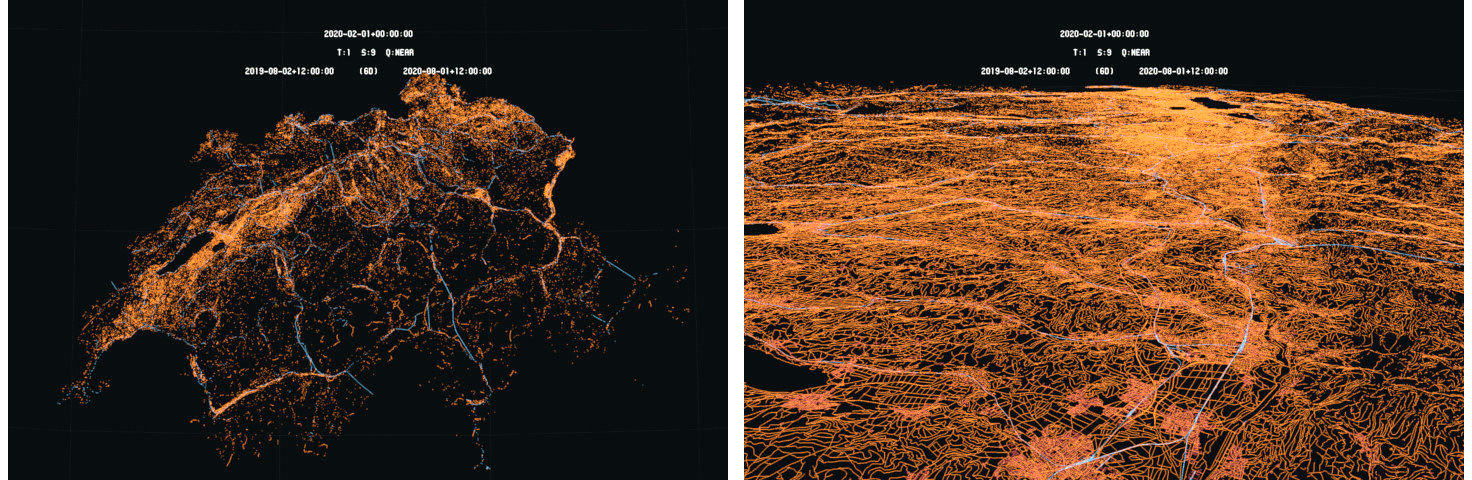
Line-based data-sets : Switzerland - Data : OSM

The following table gives a summary of the models sizes and primitives count :

Model	Size (UV3)	Primitive Count
Frauenfeld	5.0 Mio	93.3 K-Lines
Neuchâtel	33.1 Mio	620.2 K-Lines
Switzerland	1.3 Gio	25.0 M-Lines

In order to simulate evolution of the territory in time, synthetic variations are added to these models. A script is developed and used to insert controlled variations on selected primitives. The script works by randomly selecting a user-defined amount of primitives of a model and by adding a variation on one of its vertex position using a user-specified amplitude. The variation is applied on the three dimensions of space.

Vector Models : Triangle-based

A second set of triangle-based models is also considered for implementing and validating the difference detection algorithm. The selected model is a mesh model of the Swiss buildings provided by swisstopo. It comes aligned in the CH1903+ frame with elevations. It is simply converted into the WGS84 frame using again the EGM96-5 geoid model :

Triangle-based data-sets : Switzerland - Data : swisstopo

The following table gives a summary of the models sizes and primitives count :

Model	Size (UV3)	Primitive Count
Frauenfeld	116.9 Mio	1.4 M-Triangles
Neuchâtel	842.2 Mio	10.5 M-Triangles
Switzerland	30.5 Gio	390.6 M-Triangles

These models are very interesting for difference detection as the ratio between primitive size and model amplitude is very low. It means that all the primitives are small according to the model coverage, especially for the Switzerland one.

The developed script for line-based models is also used here to add synthetic variations to the models primitives in order to simulate an evolution of the territory.

Models : Statistical Analysis

Before using the models in the following developments, a statistical analysis is performed on the two Switzerland models, line and triangle-based. Each primitive of these two models are considered and their edges size are computed to deduce their distribution :

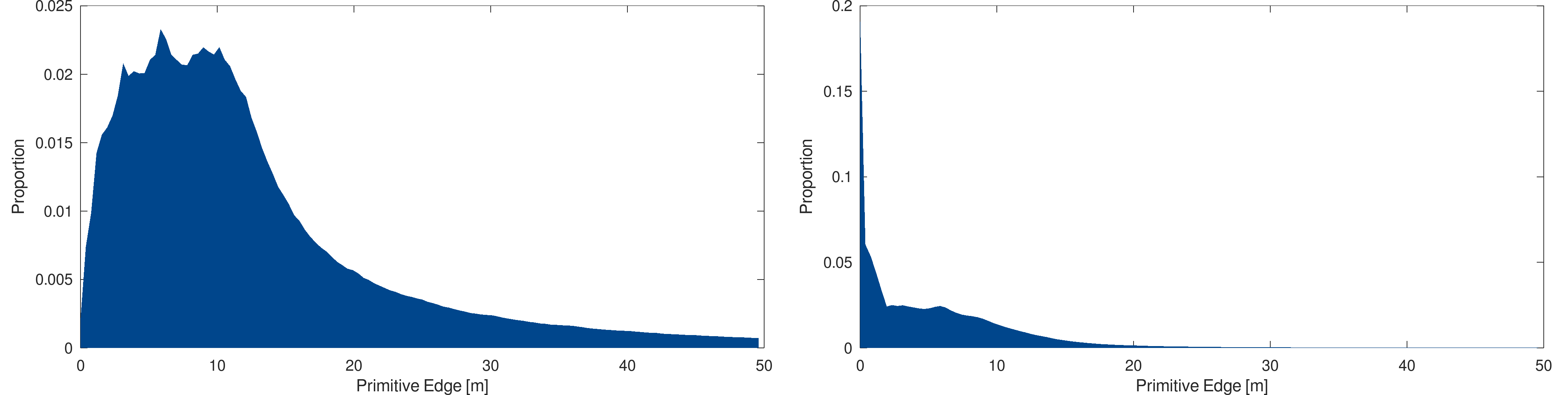
Statistical analysis : Models primitive edge size distribution, in meters, for the Switzerland models : line-based (left) and triangle-based (right)

One can see that the line-based model comes with a much more broad distribution of the primitives size. Most of the model is made from lines between zero and twenty meters. In the case of the triangle-based models, the primitives are much smaller. As most of them are less than ten meters, a significant fraction of primitives is below one meter.

Implementation of the Algorithm

In order to compare two models at two different positions in time to detect differences, the solution is of course to search for each primitive of the primary time if it has a corresponding one in the secondary time. In such case, the primitives can be concluded as static in time and only the primitives that have no correspondence will be highlighted as differences.

A first approach was initially tested : a vertex-based comparison. As every primitive (points, lines and triangles) is supported by vertexes, it can be seen as a common denominator on which comparison can take place. Unfortunately, it is not a relevant approach as it leads to an asymmetric detection algorithm. To illustrate the issue, the following image shows the situation of a group of line-based primitives at two different times with an evolution on one of the primitive vertex :

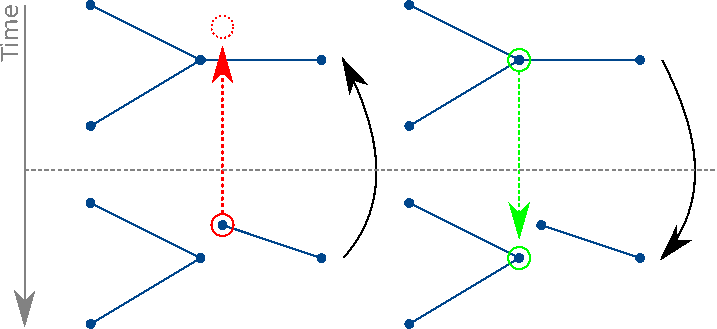
Asymmetric approach : The variation is detected only when comparing backward in time

When the comparison occurs between the second time and the first one, the modified vertex correspondence is not found, and the vertex can be highlighted as a difference. The asymmetry appears as the first time is compared to the second one. In this case, despite the primitive vertex changed, the vertex-based approach is able to find another vertex, part of another primitive, and interprets it as a vertex identity, leading the modified primitive to be considered as static.

In order to obtain a fully symmetric algorithm, that does not depend on the way models are compared in times, a primitive-attached approach is considered. The implemented algorithm then treats the correspondence problem from the whole primitive point of view, by checking that the whole primitive can be found in the other model to which it is compared to. This allows to highlight any primitive showing a modification, regardless of the way models are compared and the nature of the modification.

In addition to highlighting the primitives that changed through time, the implemented algorithm also renders the primitives that have not changed. The primitives are then shown by modulating their color to emphasize the modifications by keeping their original color for the modified one, while the static primitives are shown in dark gray. This allows to not only show the modifications but also to keep the context of the modifications, helping the user to fully understand the nature of the territory evolution.

In addition to color modulation, a variation of difference rendering is analyzed. In addition to color modulation, a visual and artificial marker is added to ease their search. The visual marker is a simple line emanating from the primitive and goes straight up with a size of 512 meters. Such markers are introduced to ease the detection of small primitives that can be difficult to spot according to large point of views.

Additional developments were required for triangle-based models : indeed, such models need to be subjected to a light source during rendering for the user to understand the model (face shading). The previously implemented lighting model is then modified to take into account color modulation in order to correctly render the triangle that are highlighted. Moreover, the lighting model was modified to light both face of the triangles in order to light them regardless of the point of view.

In addition, as mesh models are made of triangles, primitives can hide themselves. It can then be difficult for the user to spot the highlighted primitives as they can be hidden by others. An option was added to the rendering client allowing the user to ask the rendering of triangles as line-loops or points in order to make them transparent. Finally, an option allowing the user to enable or disable the render face culling was added for him to be able to see the primitive from backward.

Results and Experiments

With the implemented algorithm, a series of experiments are conducted in order to validate its results and to analyze the efficiency of the difference detection and rendering from a user point of view. In addition, experiments are also conducted to quantify the efficiency of the difference detection for automated processes.

Difference Detection : Overview

Considering the selected data-sets, each original model is injected at a given time and synthetic variations are added to a copy of it to create a second model injected at another time. The synthetic variations are randomly added to a small amount of primitives of the original model and are of the order of one meter. On the following examples, the detection is operated considering the original model as primary and the modified one as secondary.

The following images show examples of how the detection algorithm allows to highlight the detected differences while keeping the rest of the model using a darker color in case of line-based models :

Example of difference detection on line-based Frauenfeld (left) and Neuchâtel (right) models - Data : OSM

One can see how the modified primitives are highlighted while keeping the context of the modifications. The highlighted primitive is the one belonging to the primary time. Comparing the models in the other way around would lead the secondary model primitives to be highlighted.

Considering the Frauenfeld example, the following images show the situation in the primary time (original model) and the secondary time (model with synthetic variations) :

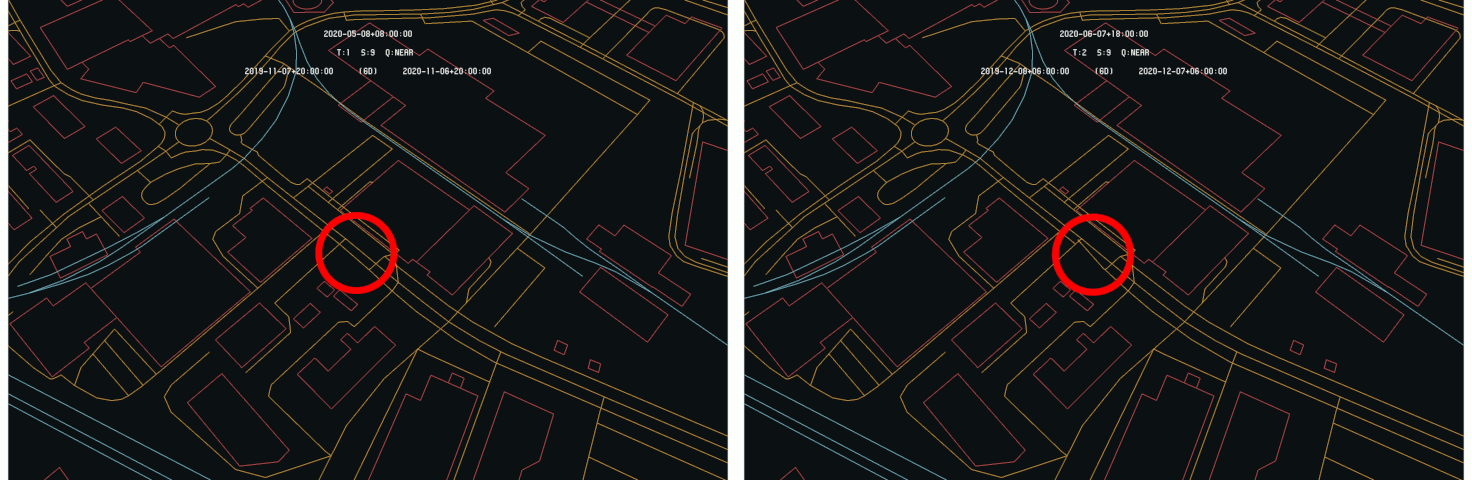
Primary model (left) and secondary one (right) showing the formal situations - The modified primitive is circled in read - Data : OSM

As a result, the user can choose between the differences highlighting with the choice of model as primary and can also switch back and worth between the models themselves though the platform interface.

Of course, the readability of the difference detection models depends on the size of the modified primitive and the scale at which the model is looked at by the user. If the user adopts a large scale point of view, the differences, even highlighted, can become difficult to spot. This issue can be worsened as triangle-based models are considered. In addition to primitive size, triangles also bring occlusions.

The visual markers added to the highlighted primitives can considerably improve ease of differences search by the user. The following images give an example of difference detection without and with the visual markers added by the algorithm :

Example of highlighted primitives without (left) and with (right) visual markers - Data : OSM

Considering the triangle-based models, difference detection is made more complicated by at least three aspects : the first one is that 3D vector models are more complex than 2D ones in the way primitives (triangles) are more densely packed in the same regions of space in order to correctly model the buildings. The second one is that triangles are solid primitives that bring occlusions in the rendering, hiding other primitives. The last aspect is that such a model can contain very small primitives in order to model the details of the buildings. In such a case, the primitives can be difficult to see, even when highlighted.

The following images show an example of highlighted triangles on the Frauenfeld model :

Example of highlighted primitive on the Frauenfeld building model - Data : swisstopo

On the right image above, the highlighted triangle is underneath the roof of the house, forcing the user to adopt an unconventional point of view (from above the house) to see it. In addition, some primitives can be defined fully inside a volume close by triangles, making them impossible to see without going inside the volume or playing with triangle rendering mode.

In such a context, the usage of the visual markers become very important for such models coming with large amount of occlusion and small primitives :

Example of highlighted primitives without (left) and with (right) visual markers - Data : swisstopo

In case of triangle-based models, the usage of markers appears to be mandatory in order for the user to be able to locate the position of the detected differences in a reasonable amount of time.

Difference Detection : User-Based Experiments

In any case, for both line and triangle-based models, the difference detection algorithm is only able to highlight visible primitives. Depending on the point of view of the user, part of the primitives are not provided by the platform because of their small size. Indeed, the whole point of the platform is to allow the user to browse through arbitrary large models, which implies to provided only the relevant primitives according to its point of view.

As a result, the detection algorithm will not be able to highlight the variations as the involved primitives are not considered as a query answer by the platform. The user has then to reduce is point of view in order to zoom on the small primitives to make them appear, and so, allowing the algorithm to highlight them.

In order to show this limitation, an experiment is performed. For each model, a copy is made on which eight synthetic differences are randomly introduced. The variations are of the order of one meter. The models and their modulated copy are injected in the platform. The rule is the following : the user uses the detection algorithm on each model and its modulated copy and has five minutes to detect the eight differences. Each time a difference is seen by the user, the detection time is kept. The user is allowed to use the platform in the way he wants. In each case, the experiment is repeated five times to get a mean detection rate.

As one could ask, these measures are made by the user and are difficult to understand without a reference. In order to provide such reference, the following additional experiment is conducted : each model and its modulated copy are submitted to a naive automated detection process. This process parses each primitive of the original model to search in its modulated copy if the primitive appear. If the primitive is not found, the process trigger a difference detection. This process is called naive as it simply implements two nested loops, which is the simplest searching algorithm implementation. The process is written in C with full code optimization and executed by a single thread.

Starting with the line-based models, the following figures shows the difference detection rates according to time. For each of the three models, the left plots show the rate without visual markers, the middle ones with visual markers and the right ones the naive process detection rate :

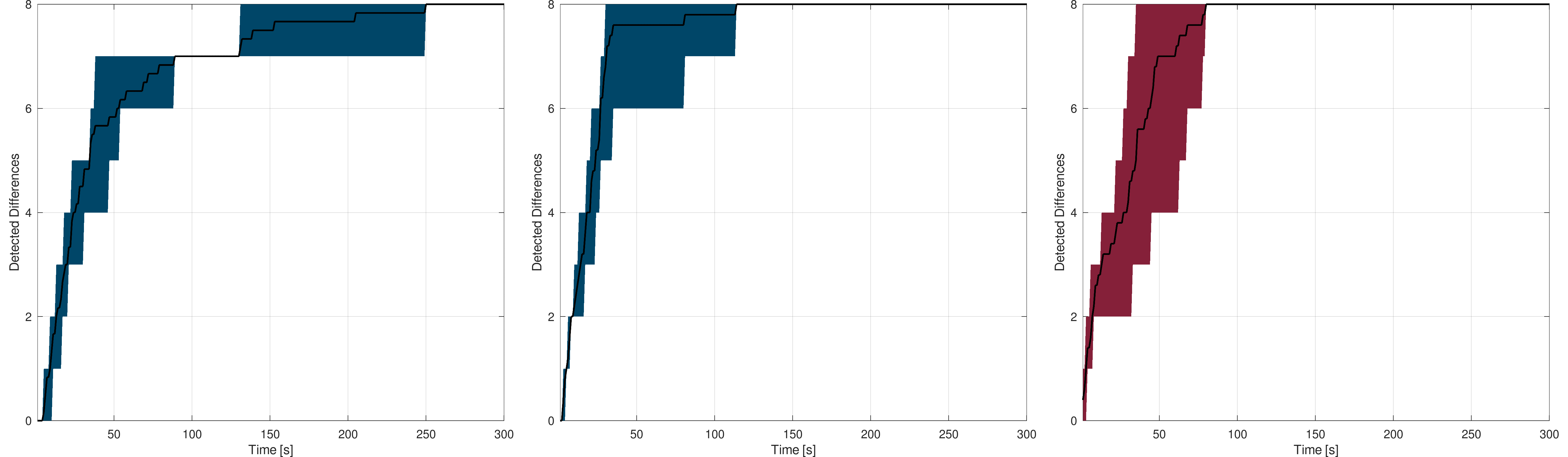
Frauenfeld : The black curve shows the mean detection rate while the blue (left, middle) and red (right) area gives the worst and best rates
Left : without visual markers - Middle : with visual markers - Right : automated process

Canton of Neuchâtel : The black curve shows the mean detection rate while the blue (left, middle) and red (right) area gives the worst and best rates
Left : without visual markers - Middle : with visual markers - Right : automated process

Switzerland : The black curve shows the mean detection rate while the blue (left, middle) and red (right) area gives the worst and best rates
Left : without visual markers - Middle : with visual markers - Right : automated process

As expected, the larger the model is, the more difficult it is for the user to find the highlighted differences, with or without visual markers. Considering a city, the differences, even of the order of one meter, are easy to spot quickly. As the model gets larger, the more time it takes for the user to find the differences. On a model covering a whole canton (Neuchâtel), one can see that most of the differences are detected in a reasonable amount of time despite their small size according to the overall model. On the Swiss model, things get more complicated, as simply looking at each part of the country is already complicated in only five minutes, leading the detection rate to be lower, even using the visual markers.

These results are consistent with the statistical analysis made on the line-based Switzerland model. Detection on a city or even a whole canton lead the user to adopt a point of view sufficiently close to make most of the primitives appearing. For the Switzerland model, the user is forced to adopt a larger point of view, leading to a significant proportion of primitives to stay hidden.

These results also show that adding visual markers to the highlighted primitives increases the user detection rate, meaning that the markers lead to a more suitable rendering from the user experience point of view.

Considering the user results and the naive detection process, one can see that the user obtains at least similar results but most of the time outperforms the automated process. This allows to demonstrate how the implementation and data broadcasting strategy of the platform is able to provide an efficient way to access models and composite models, here in the context of difference detection.

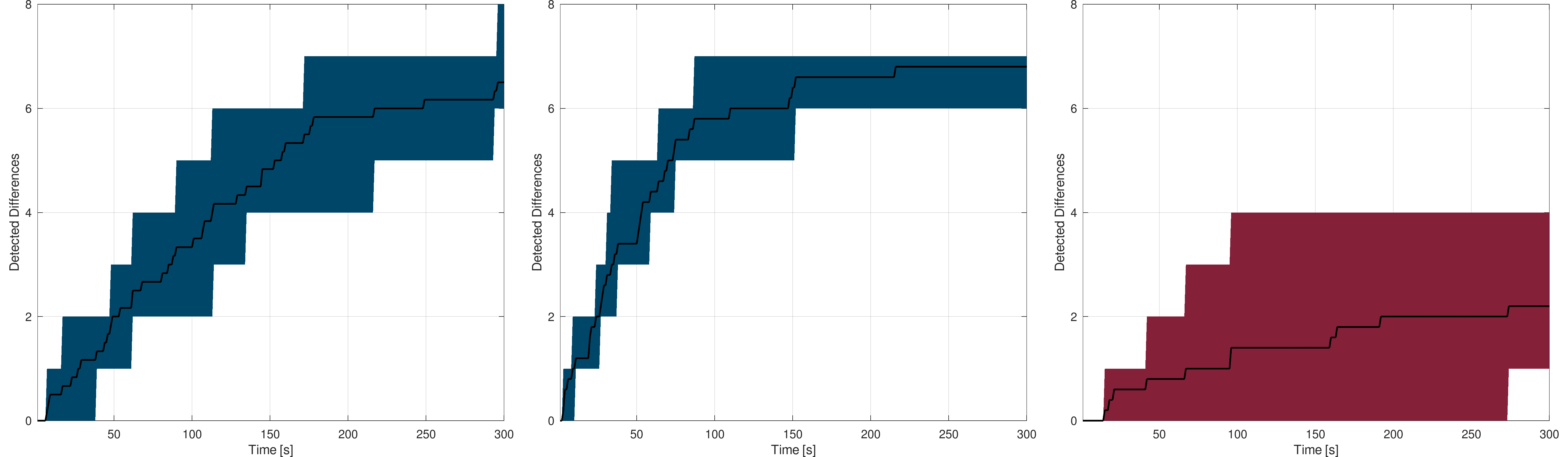
The following figures show the experiments results for the triangle-based models, which were not performed on the whole Switzerland model due to limited rendering capabilities :

Frauenfeld : The black curve shows the mean detection rate while the blue (left, middle) and red (right) area gives the worst and best rates
Left : without visual markers - Middle : with visual markers - Right : automated process

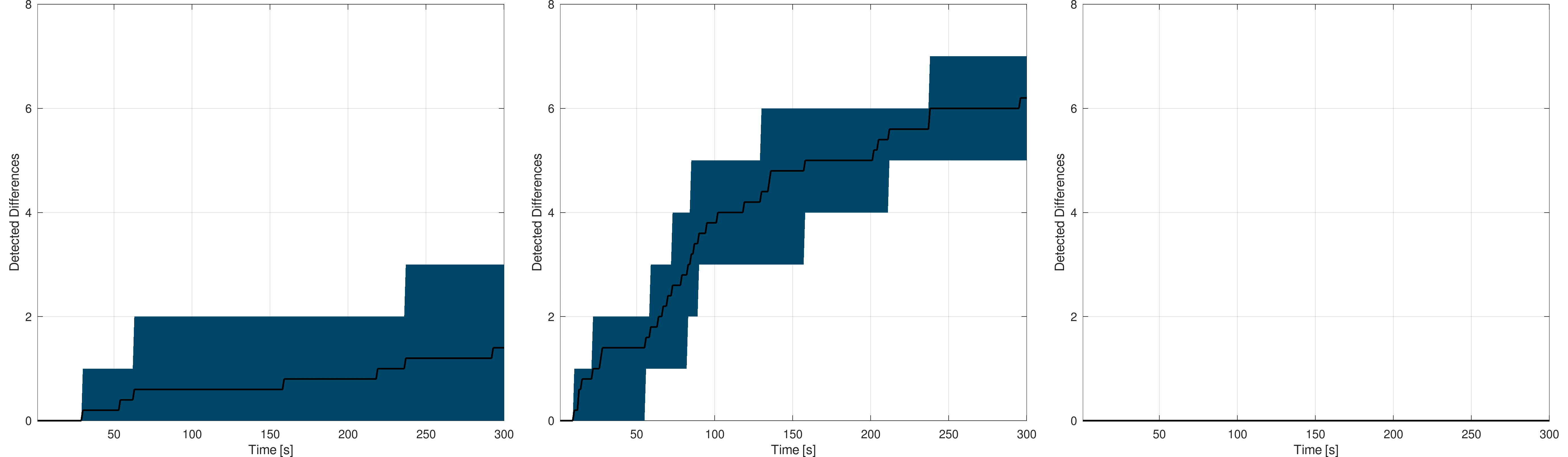
Canton of Neuchâtel : The black curve shows the mean detection rate while the blue (left, middle) and red (right) area gives the worst and best rates
Left : without visual markers - Middle : with visual markers - Right : automated process

Similar conclusions apply for the triangle-based models : the larger the model is, the more difficult the difference detection is. These results also confirm that adding visual markers in addition to primitives highlighting significantly helps the user, particularly in case of triangle-based models.

The obtained results on triangle-based models are lower than for line-based models. A first explanation is the greater amount of primitive that lead the user to spend more time at each successive point of view. The occlusion problem also seems to play a role, but to a lesser extent as the visual markers seems to largely solve it. The differences between detection on line and triangle-based models have to be searched in the statistical analysis of the triangle-based models. Indeed, for these models, a large proportion of the primitives are very small (less than a meter), leading them to be rendered only as the user adopts a close point of view, making the detection much more complicated in such a small amount of time.

The triangle-based models being larger than the line-based one, the results of the naive process are very poor. As for the line-based models experiments, the user outperforms this automated process, in a much more significant way.

Difference Detection : Process-Based Experiments

In the previous experiments, the user ability to find the differences on the data-sets, using synthetic variations, was benchmark in perspective of the results provided by a naive automated process. The user performs quite well using the platform, but start to struggle as the data-sets get bigger according to the sizes of their primitives.

In this second set of experiments, the platform is used through an automated process instead of a user. The process has the same task as the user, that is, finding the eight synthetic differences introduced in the models copy. The process starts with a list of index (the discretization cells of the platform) in order to query the corresponding data to the platform before to search for differences in each cell. The process implements, then, a systematic difference detection covering the whole model.

In order for the process to work, it requires an input index list. To create it, the primitive injection condition of the platform is used to determine the maximal depth of these index. The following formula gives the poly-vertex (lines and triangles) primitives injection condition according to the platform scale. In other words, the formula gives the shallowest scale at which the primitive is considered through queries according to its size :

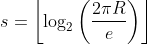
where s gives the shallowest scale, R being the WGS84 major semi-axis and e is the largest distance, in meters, between the primitive first vertex and its other ones. For example, choosing s = 26 allows the index to reach any primitive that is greater than ~30 cm over the whole model covered by the index.

The scale 26 is then chosen as the deepest search scale in the following experiments. This value can be adapted according to the primitives size and to the nature of the detection process. The larger it is, the more data are broadcast by the platform increasing the processing time.

In order to compare the user-based experiments, the naive automated approach and this process-based exhaustive search, the same protocol is considered. The process addresses queries to the platform, based on the index list, and save the detection time of each difference. The detection rate is plot in the same way as for the previous experiments. Again, eight synthetic differences are randomly introduced and the experiment is repeated five times for the line-based model and only two times for the triangle-based model.

As the scale 26 is chosen as the deepest search scale, the index list can be built in different ways. Indeed, as a query is made of one spatial index, that points at the desired cell, and an additional depth (span), to specify the density of data, the only constraint to maintain the deepest search scale at 26 is the following :

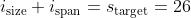
where the two left hand side terms are the spatial index size and span value. In these experiments, a first list of index is built using a span of 9 and a second with a span of 10. As the deepest scale is maintained constant, increasing the span reduces the index list size, but the queried cells contain more data to analyze.

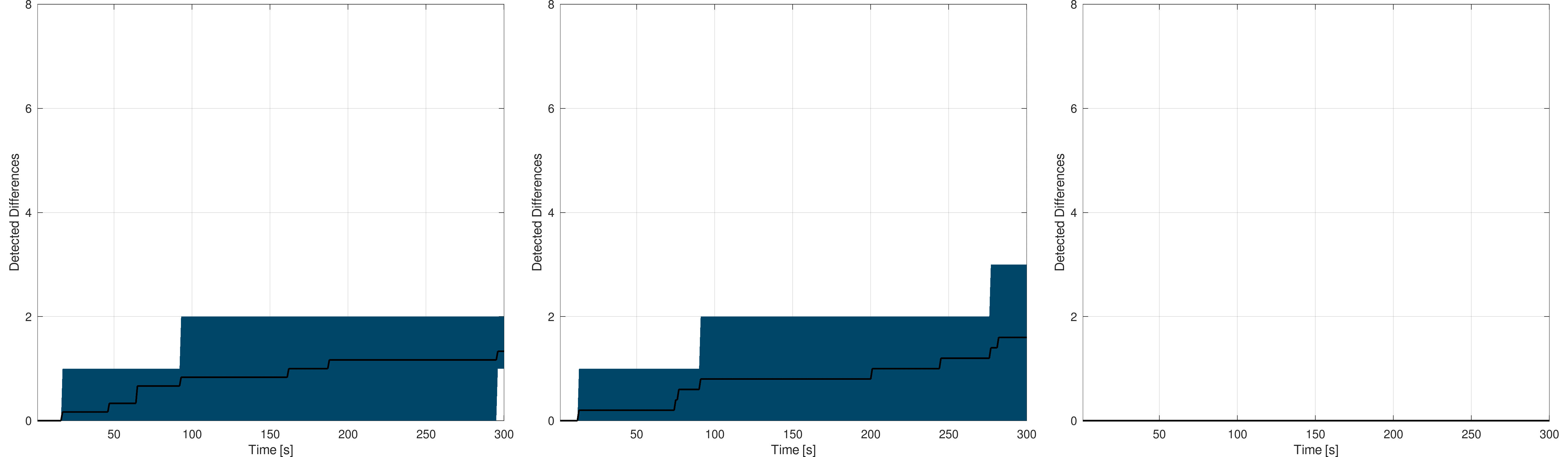
The following figures show the mean detection rate for the Switzerland lined-based model with the deepest scale at 26 and span at 9 and 10. The plots are scaled in the same way as for the user-based experiments :

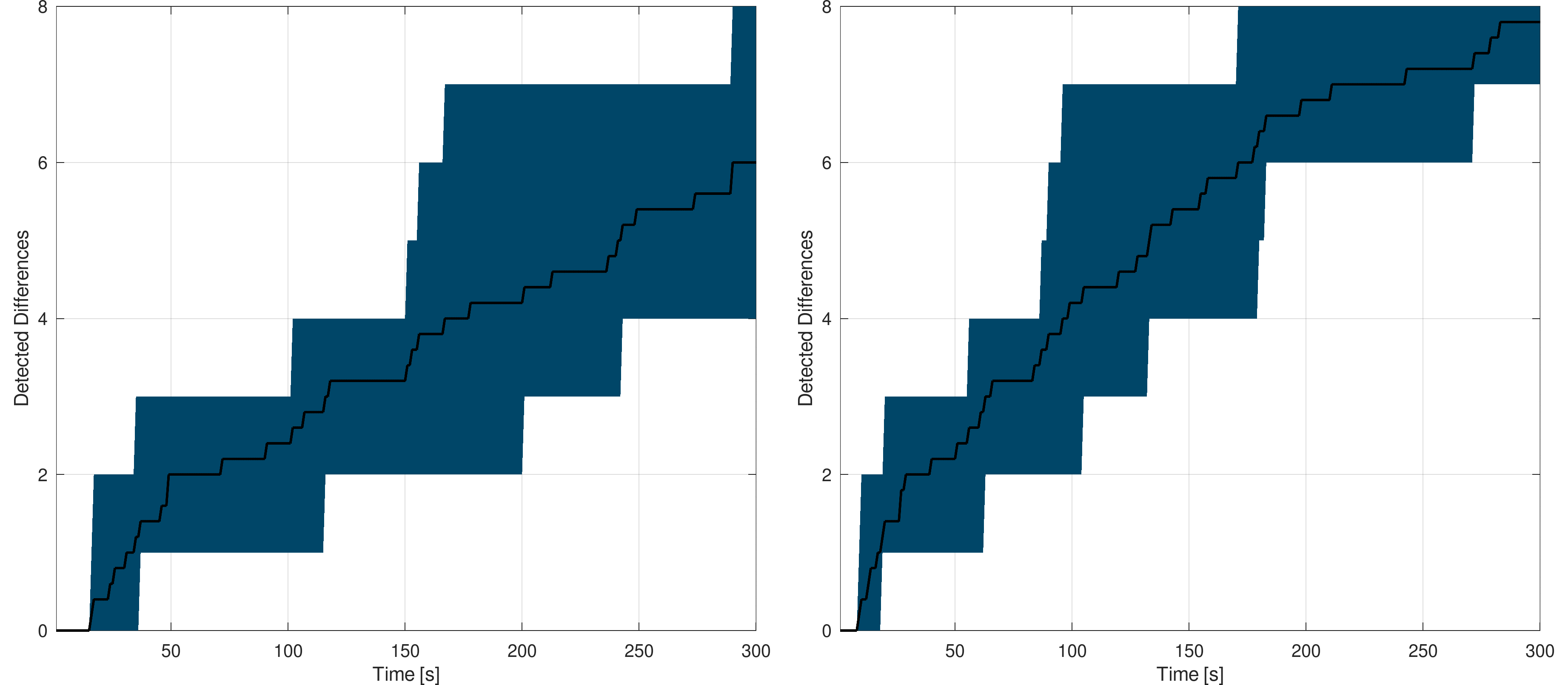
Switzerland : The black curve shows the mean detection rate while the blue area gives the worst and best rates - Span at 9 (left) and 10 (right)

One can see that the detection rate on such a model is much better than the user-based or naive approach ones. In a manner of five minutes, for the span set to 10, the eight differences can be detected and reported. The full detection process took ~5 minutes with span set to 10 and ~8 minutes with the span set to 9. This shows how the platform can be used by automated processes as an efficient data provider. In addition, as the data are queried by the automated process, the detected primitive geometry is directly available, allowing all sorts of subsequent processes to take place.

As the deepest scale was set to 26, in one of the five measures session, one of the eight differences was not detected (at all). It means that the primitive on which a synthetic variation was introduced is smaller than 30cm and was then not reached by any index. This shows the importance of defining the spatial index and spans according to the processes needs. For example, increasing the deepest scale to 27 would allow reaching primitive down to ~15 cm over the whole Switzerland, and so on.

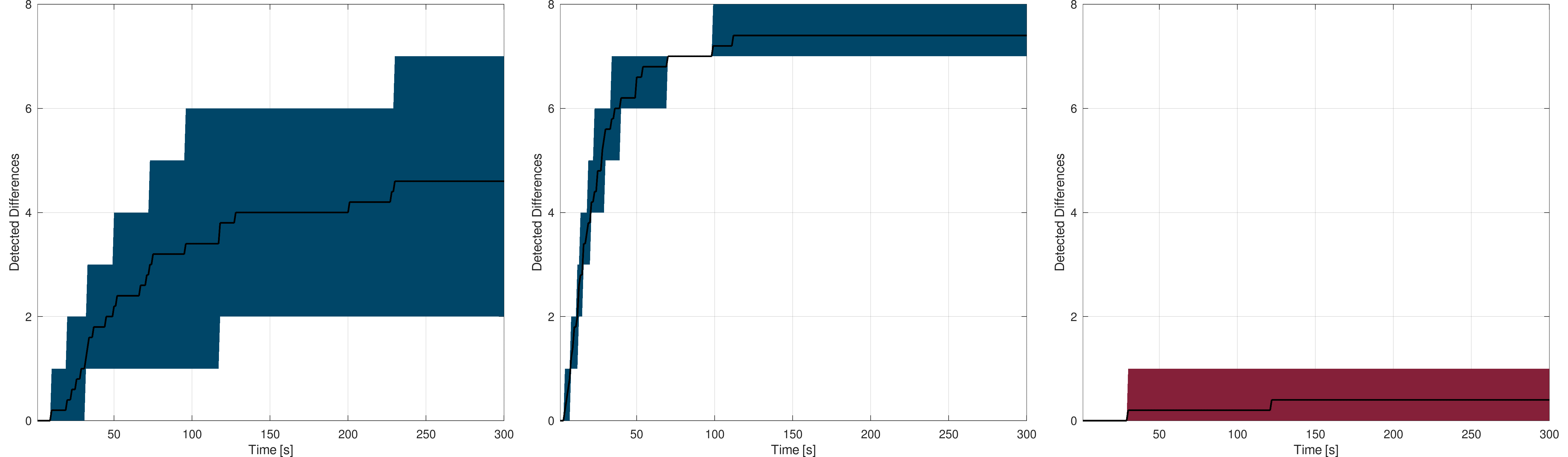
The following figures show the mean detection rate for the Switzerland triangle-based model. In this case, only two measure sessions were made to limit the time spent on this analysis :

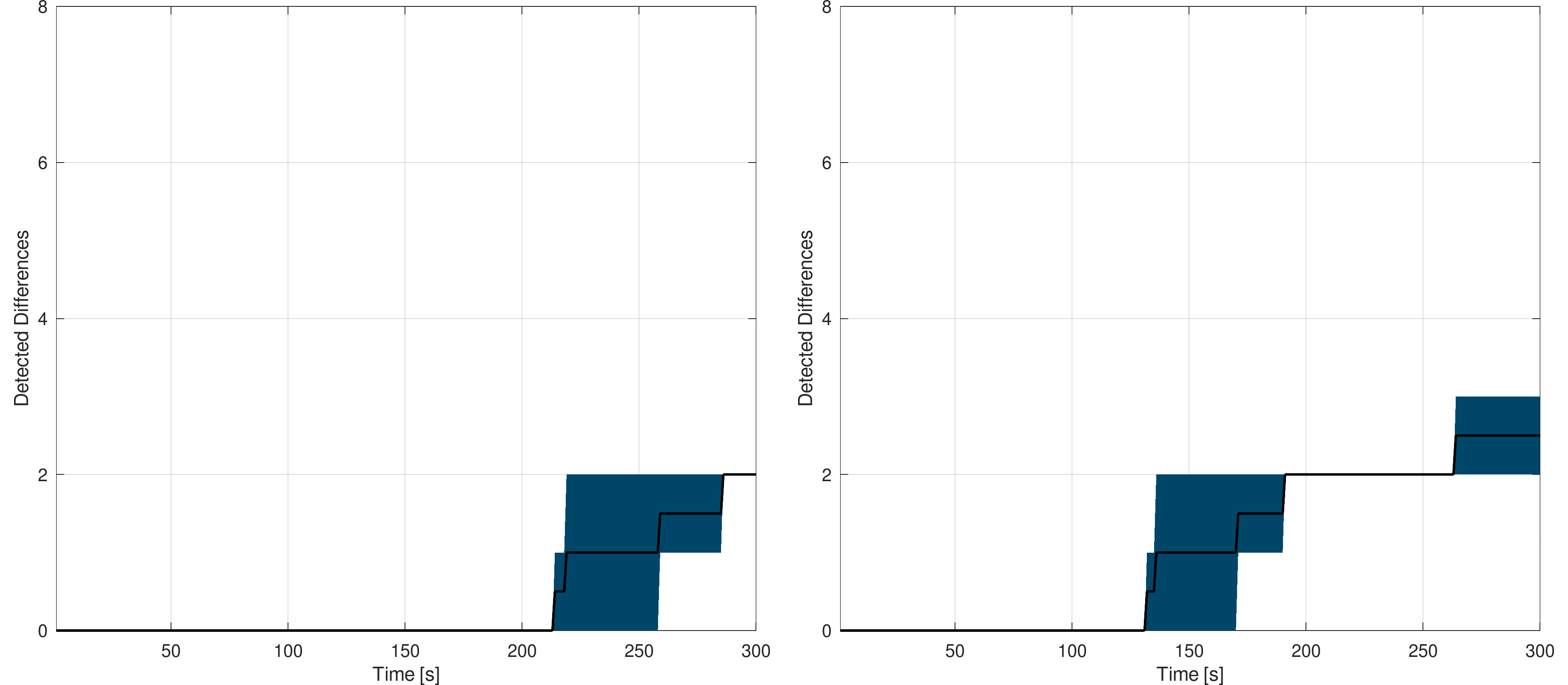
Switzerland : The black curve shows the mean detection rate while the blue area gives the worst and best rates - Span at 9 (left) and 10 (right)

The conclusion remain, but the rate is slower in this case as the model contains much more primitives than the line-based one. In this case, the full detection process took ~15 minutes with span set to 10 and ~20 minutes with the span set to 9. Again, in one of the two measure session, one difference was not detected due to the size of the primitive. Nevertheless, these results shows how the platform, seen as a process data provider, allows outperforming user-based and classic detection algorithms.

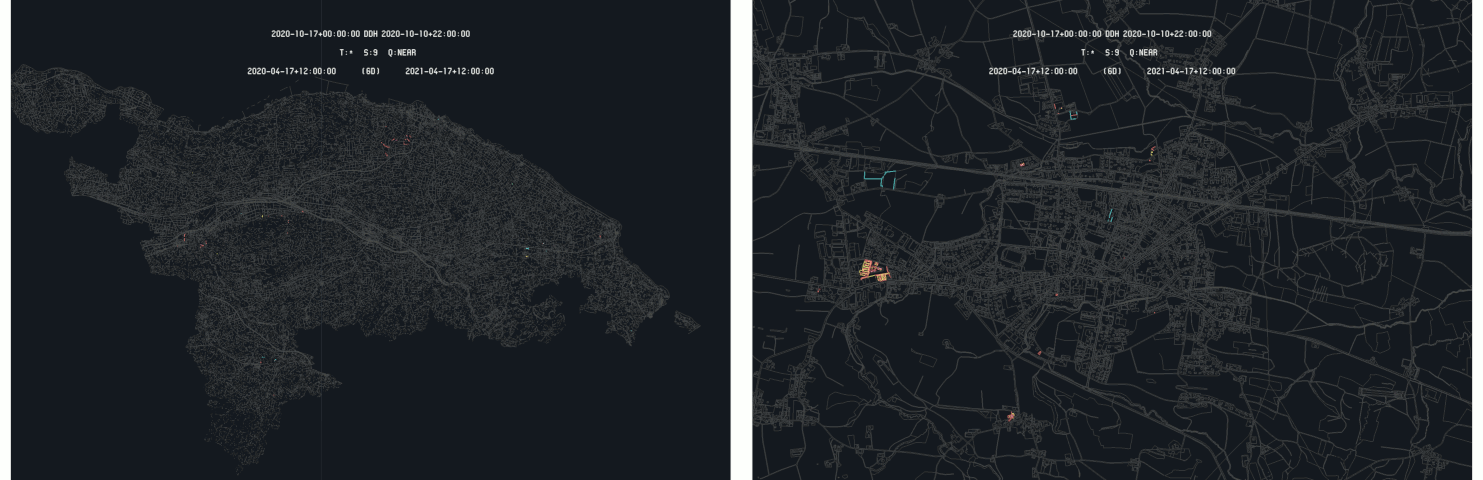
Such process-based strategy can be performed in many ways depending on the needs. For example, the index list can be limited to a specific area or set to focus on spread and defined locations (for example at the intersection of the Swiss hectometric grid). The following image gives a simple example of how the detected differences can be leveraged. As the geometry of the differences is known by the process, a summary of the differences can be provided through a simple map :

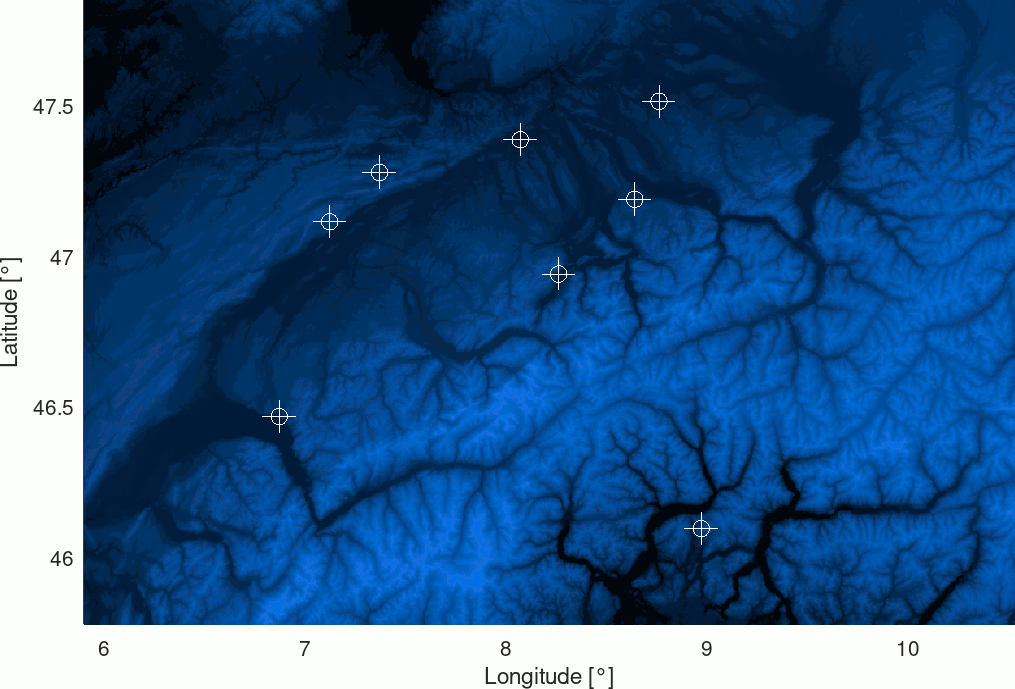
Example of a differences map based on the results of the detection process - Data : SRTM

The eight synthetic differences are easily presented allowing a user to analyze them more in detail in the platform interface for example. This map was created detecting the eight differences on the line-based Switzerland model in about 5 minutes with a span set to 10.

Conclusion : First Phase

During this first phase, the difference detection algorithm was developed and validated on both line-based and triangle-based data. An efficient algorithm is then implemented in the platform allowing emphasizing differences between models at different temporal positions. The algorithm is able to perform the detection on the fly with good performances allowing the users to dynamically browse the data to detect and analyze the territory evolutions.

The performances of the detection algorithm allow the platform to be suitable for automated detection processes, as a data provider, answering large amounts of queries in an efficient and remote manner.

Two variations of the difference detection algorithm are implemented. The first version consists in highlighting the primitives that are subject to modifications over a time. This variation is suitable for automated processes that can rely on simple search methods to list the differences.

For the users, this first variation can lead to more difficult visual detection of the differences, especially in case the highlighted primitives are small or hidden by others. For this reason, visual markers were added on top of the highlighted primitives in order to be seen from far away, regardless of the primitives size. The measures sessions made during the user-based experiments showed a clear improvement of the detection rate when using the visual markers. This was especially true for triangle-based models, where the primitives bring occlusions.

The user-based experiments showed that using the platform interface, a human can significantly outperform the result of a naive automated process operating on the models themselves. The experiments showed that the user is able to efficiently search and find through space and time the evolutions of the territory appearing in the data.

Of course, as the model size and complexity increases, the user-driven interface starts to show its limits. In such a case, the process-based experiments showed that automated processes can take over these more complicated searches through methods allowing performing exhaustive detection over wide models in a matter of several minutes.

At this point, the developments and validations of the algorithm, and its variations, were conducted on synthetic modifications introduced in models using controlled procedures. The next phase focuses on formal data extracted from land registers.

Second Phase : True Variations

In this second phase, also dedicated to vector-based models, the focus is set on applying the developed difference detection algorithm on true land register models. Two sets of data are considered in order to address short-term and long-term difference detection.

Selected Resources and Models

In both cases, short-term and long-term, INTERLIS data are considered. A selection of tables in different topics is performed to extract the most interesting geometries of the land registering. For all models, the following colors are used to distinguish the extracted layers :

INTERLIS selected topics and tables colors - Official French and German designations

The layers are chosen according to their geometric content. The color assignation is arbitrary and does not correspond to any official colorization standard.

Short-Term Difference Detection : Thurgau

For the short-term application of the difference detection algorithm, the case of the Thurgau canton is considered. Two set of INTERLIS data are considered that are very close in time, of the order of days. The selected layers are extracted from the source files before to be converted to the WGS84 frame using the EGM95-6 geoid model. The heights are restored using the SRTM topographic model. The following images give an illustration of the considered data :

Canton of Thurgau (left) and close view of Frauenfeld (right) - Data : Kanton Thurgau

Two INTERLIS models are considered with times 2020-10-13 and 2020-10-17, corresponding to the models gathering time. The following table gives the models size and primitives count :

Model	Size (UV3)	Primitive Count
Thurgau 2020-10-13	203.7 Mio	3.8 M-Lines
Thurgau 2020-10-17	203.8 Mio	3.8 M-Lines

As the two models are very close in time, they are very similar in size and content as the corrections count made during the considered time range is small.

Long-Term Difference Detection : Geneva

For the long-term difference detection analysis, the Geneva case is selected as the canton of Geneva keeps a copy of each land register model for each month from at least 2009. This allows to compare INTERLIS models that are further away from each other from a temporal point of view. The selected layers are extracted and converted to the WGS84 coordinates system using the EGM96-6 geoid model. Again, the SRTM model is used to restore the heights. The following images give an illustration of the selected models :

Canton of Geneva in 2019-04 (left) and close view of Geneva in 2013-04 (right) - Data : SITG

The selected models are not chosen randomly along the time dimension. Models that corresponds to the Geneva LIDAR campaigns are selected as they are used in the next phase. In addition, as the LIDAR campaigns are well spread along the time dimension, the selected models are far away from each other in time, of the order of at least two years. The following table summarize the models size and primitives count :

Model	Size (UV3)	Primitive Count
Geneva 2009-10 (MN03)	550.2 Mio	10.3 M-Lines
Geneva 2013-04	407.0 Mio	7.6 M-Lines
Geneva 2017-04	599.6 Mio	11.2 M-Lines
Geneva 2019-04	532.6 Mio	9.9 M-Lines

As the temporal gaps between the models are much larger than for the Thurgau models, the size and primitive count show larger variations across the time, indicating that numerous differences should be detected on these data.

Models : Statistical Analysis

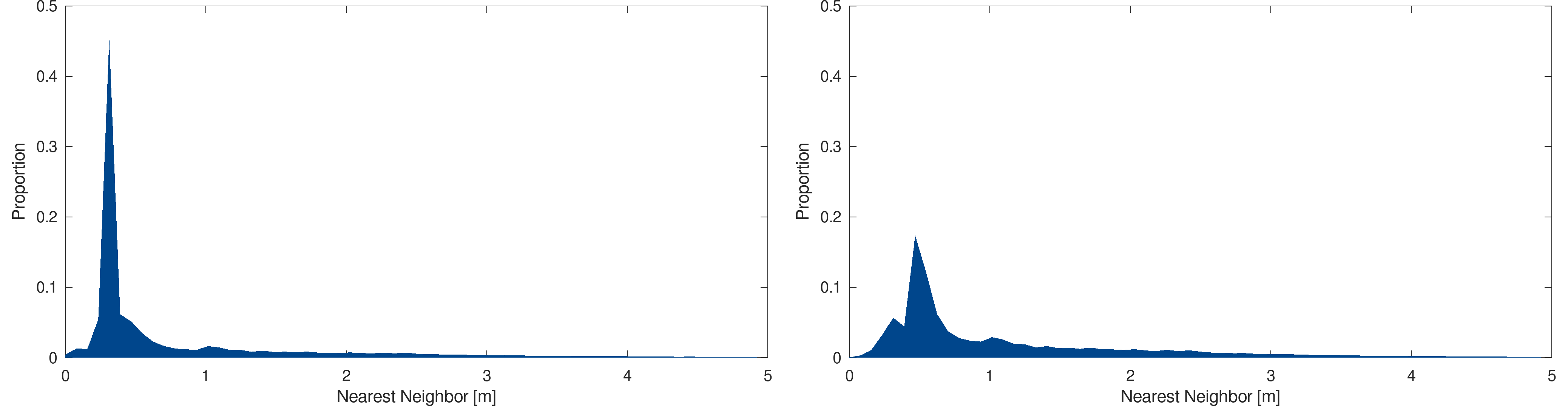
As in the first phase, a statistical analysis of the Thurgau and Geneva models is conducted. The following figures show the line length distribution of the two Thurgau models :

Statistical analysis : Primitive size distribution, in meters, for the Thurgau 2020-10-13 (left) and 2020-10-17 (right)

As expected, as the models are very similar, the distribution between both models is almost identical. In both cases, the distribution is centered around two meters and is mostly contained within the [0,5] range. The following figures show the same statistical analysis for the Geneva models, more spread along the time dimension :

Statistical analysis : Primitive size distribution, in meters, for the Geneva 2009-10 (top-left), 2013-04 (top-right), 2017-04 (bottom-left) and 2019-04 (bottom-right)

One can see that the distribution varies more from a time to another. In addition, in comparison with the Thurgau models, the Geneva models tend to have smaller primitive, mostly distributed in the [0,1] range with a narrower distribution.

Results and Analysis

Short-Term : Thurgau

In the case of Thurgau data, the models are only separated in time by a few days. It follows that only a small amount of differences is expected. As an introduction, the following images show the overall situation of the difference detection between the two models. The differences are highlighted by keeping the primitive original color while identities are shown in dark gray to allow context conservation :

Overall view of difference detection : Thurgau (right) and Amriswil (left)

As expected, as the two models are very close in time, only a limited amount of differences is detected. Such situation allows to have a clear view and understanding of each difference.

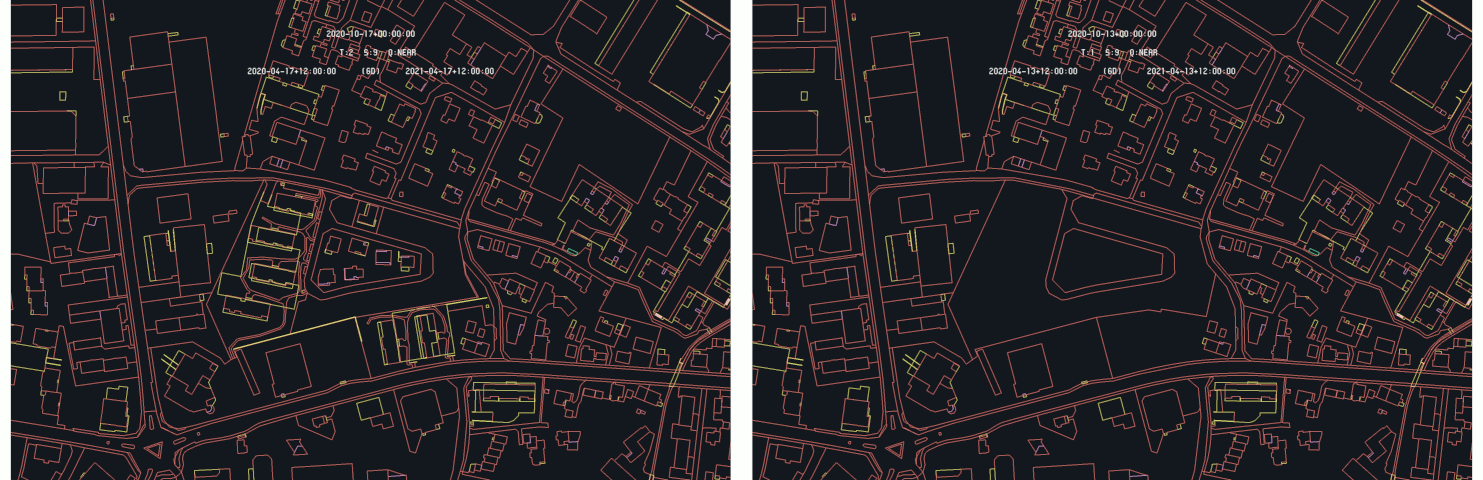
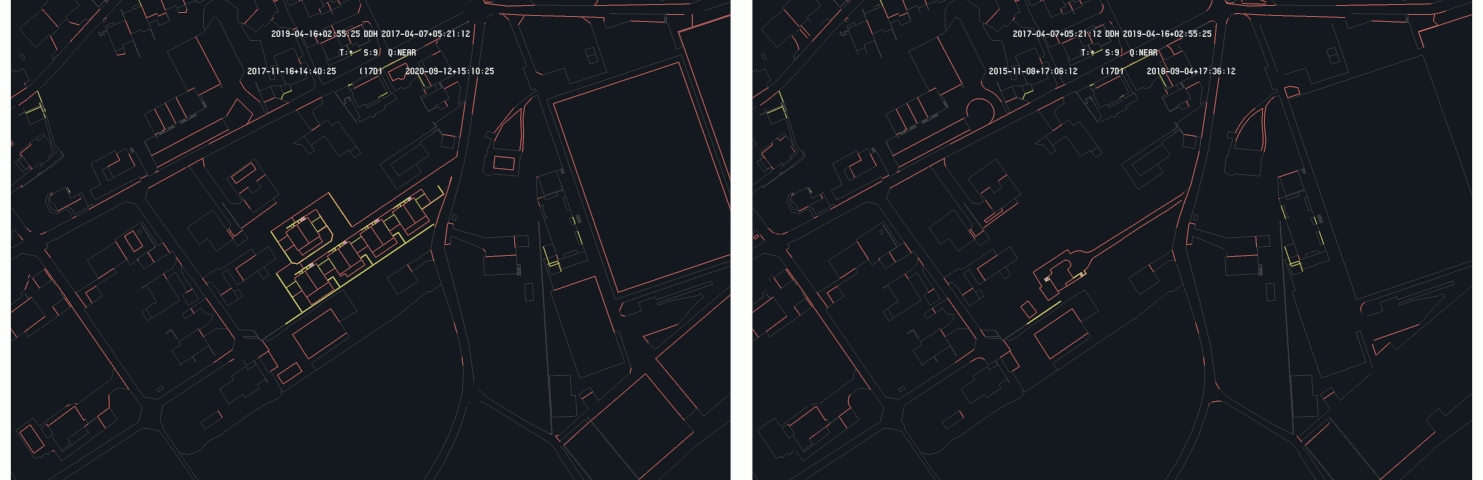
In order to analyze the results of the difference detection algorithm on real cases, selected differences, using the algorithm itself, are studied more in detail to emphasize the ability of the algorithm to detect and make the difference understandable for the user. As a first example, the case of the Bielackerstrasse in Amriswil is considered and illustrated by the following images :

Example of difference detection : Bielackerstrasse in Amriswil - 2020-10-17 (right) and 2020-10-13 (left) as primary time

In this case, new buildings are added to the official land register. As the 2020-10-17 is selected as primary, the highlighted elements correspond the footprint of the added buildings. When the 2020-10-13 time is set as primary, as it does not contain the building footprints, the highlighted elements only corresponds to the re-measured elements for land register correction. This illustrates the asymmetry of the difference detection algorithm that only highlight primitives of the primary time.

In addition, by keeping the color of the highlighted primitives, the difference detection algorithm allows to immediately see that three layers of the land register have been affected by the modification (German : Einzelobjekte, Flaechenelement Geometrie; Bodenbedeckung, BoFlaeche Geometrie; Einzelobjekte, Linienelement). The following images show the respective situation of the 2020-10-13 and 2020-10_17 models :

Situation of Bielackerstrasse in Amriswil - 2020-10-17 (right) and 2020-10-13 (left)

This confirms the analysis deduced from the difference detection algorithm that a group of new buildings are added to the land register. In this example, if the inner road was not re-measured, at least on some portion, the difference detection with 2020-10-13 as primary time would have shown noting.

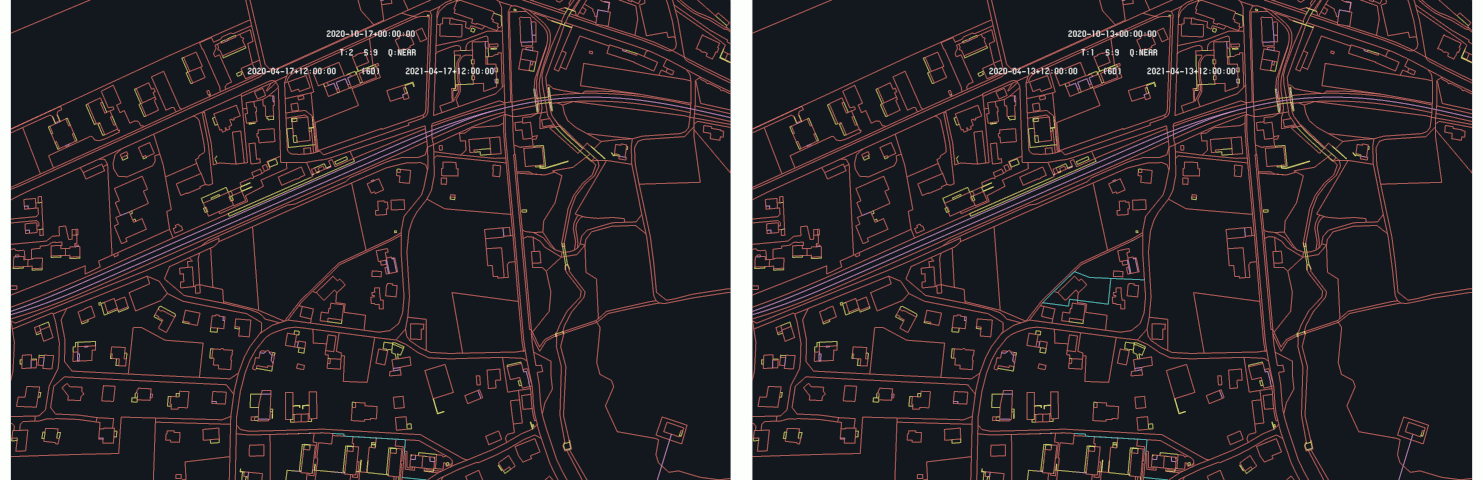
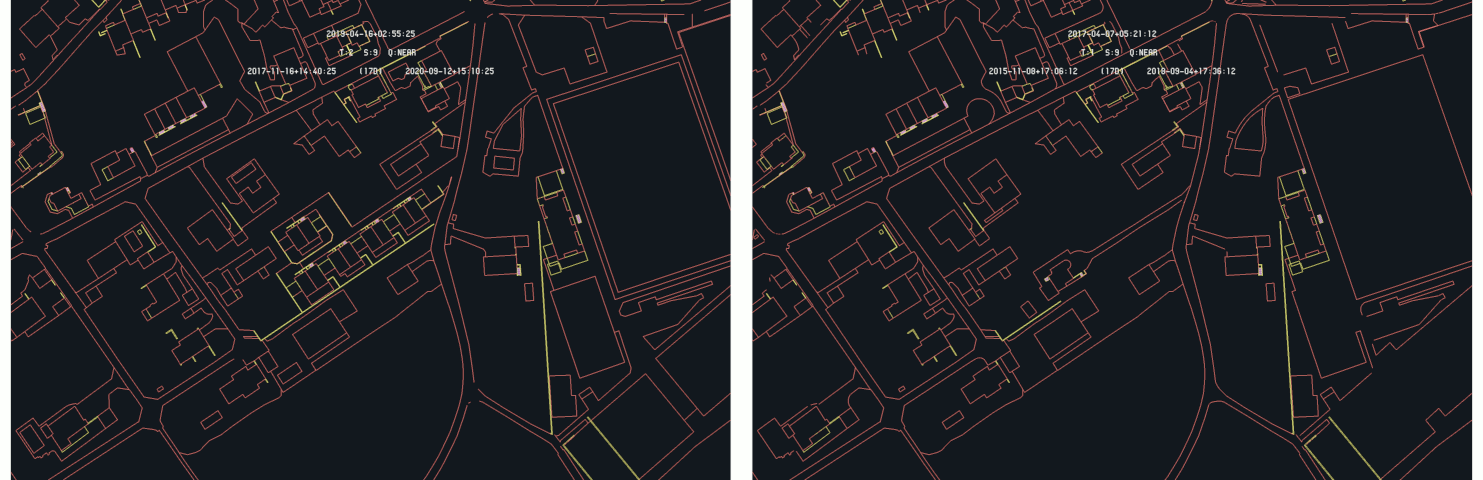
To illustrate the asymmetry of the algorithm more clearly, the example of Mammern is considered. On the following image, the result of the difference detection is illustrated with both time chosen successively as primary :

Example of difference detection : Mammern - 2020-10-17 (right) and 2020-10-13 (left) as primary time

On this specific example, one can see that choosing the 2020-10-17 time as primary, which is the most recent time, nothing is highlighted by the detection algorithm. But when the 2020-10-13 time is set as primary, a specific element appears as highlighted, showing an evolution of the land register. This example illustrates the deletion of a sequence of primitive of the property (German : Liegenschaften, ProjLiegenschaft Geometrie) layer of the land register, which then only appear as the oldest time is set as primary. The following images show both time situation :

Situation of Mammern - 2020-10-17 (right) and 2020-10-13 (left)

This example shows the opposite situation of the previous one, where elements were deleted from the land register instead of added.

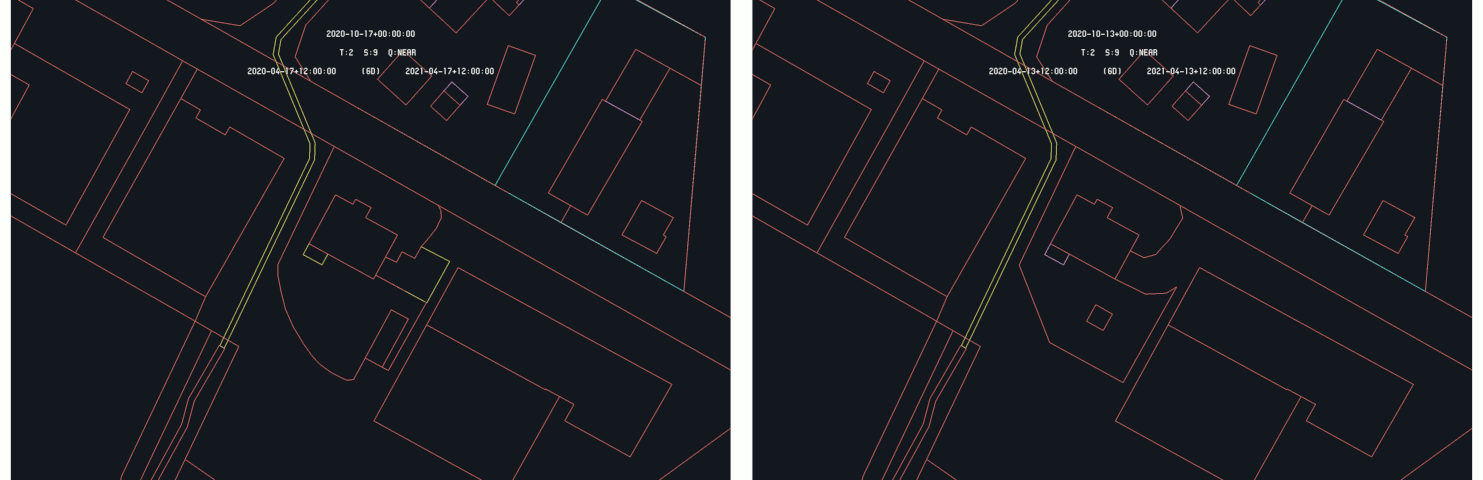
As a last example, an in-between situation is selected. The case of the Trungerstrasse in Münchwilen is considered and illustrated by the following images showing both time as primary :

Example of difference detection : Trungerstrasse in Münchwilen - 2020-10-17 (right) and 2020-10-13 (left) as primary time

This situation is in-between the two previous one as nothing really appeared and nothing really disappeared from the land register. A modification was made on the situation of this specific property and so, appear no matter which of the two times is selected as primary. The following images show the formal situation of the land register for the two times :

Situation of Trungerstrasse in Münchwilen - 2020-10-17 (right) and 2020-10-13 (left)

One can see that the correction made are around the pointed house, as the access road of the rear delimitation. For this type of situation, the algorithm recover some kind of symmetry, as the selected time as primary does is not relevant to detect the difference.

To conclude this short-term difference detection analysis, the efficiency of visual markers is illustrated on the region of Romanshorn and Amriswil on the following images. Both images show the difference detection rendering without and with the visual markers :

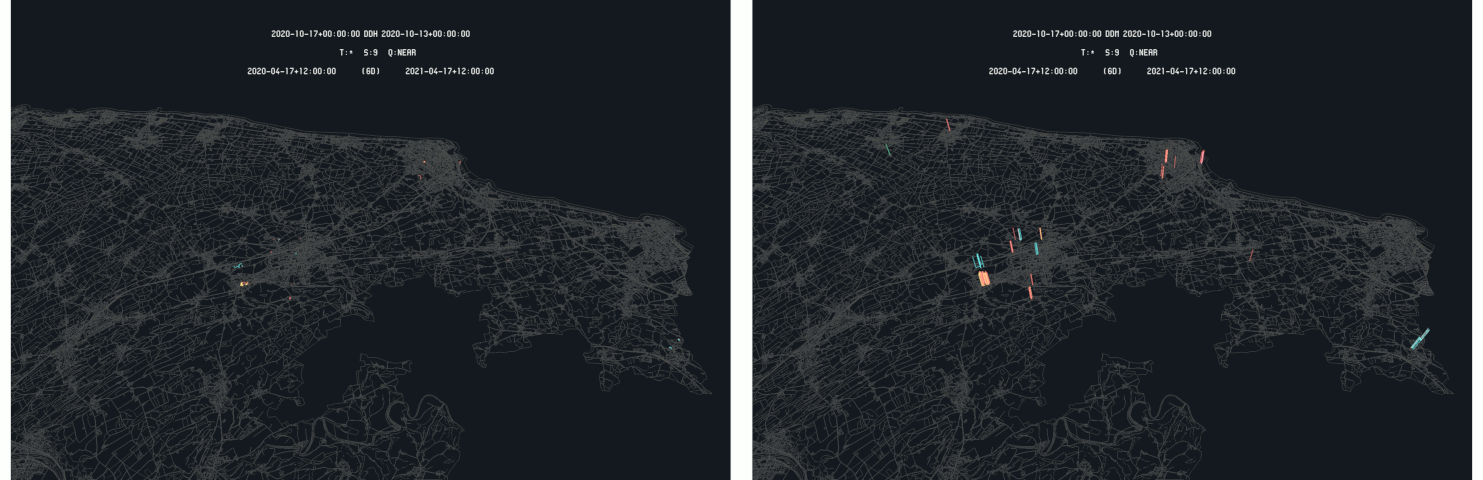
Illustration of difference detection without (right) and with (left) visual markers - 2020-10-17 as primary time for both images

One can see that, for small highlighted primitive, the usage of visual markers eases the differences view for the user. Of course, as the highlighted primitive are big enough, or if the point of view is very close to the model, the efficiency of the visual markers decreases.

Long-Term : Geneva

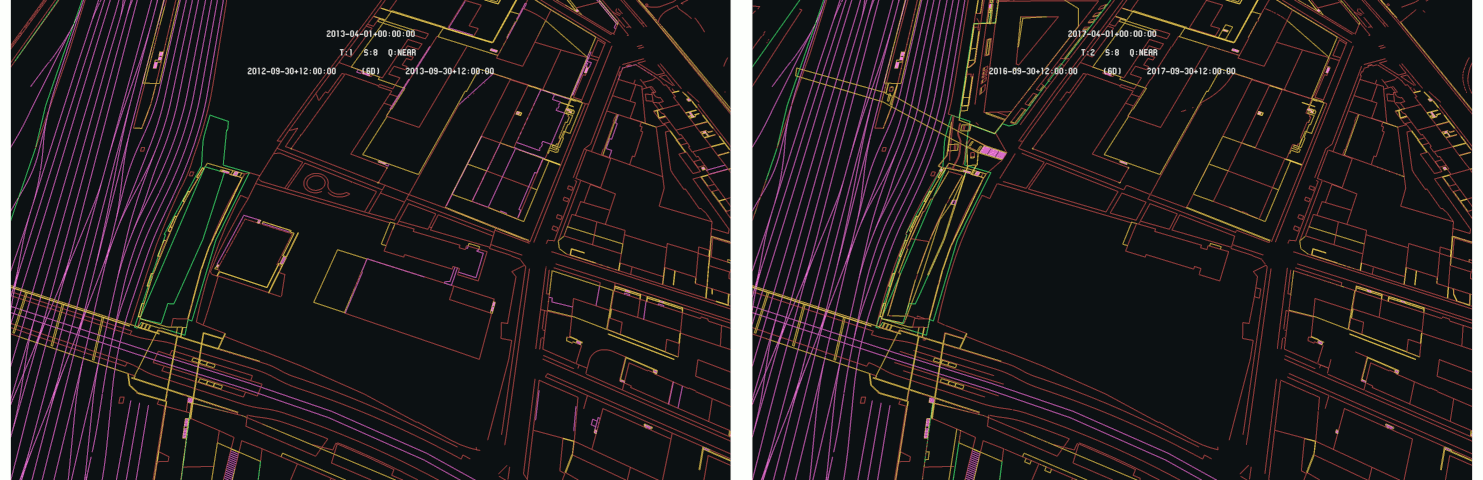
Considering the Geneva land register, the compared model are much more spread along the time dimension, leading to a much richer difference model. Starting with the 2019-04 and 2017-04 models, the following images gives an overview of the detected differences on the whole canton :

Overall view of difference detection between Geneva 2019-04 and 2017-04 models with 2019-04 as primary

On this example, one can see that a much larger amount of differences is detected as the model are separated by two years. As the first observation, one can see that large portions of the model seems to have entirely moved between the two dates. Three of these zones are clearly visible on the images above as all their content is highlighted by the difference detection algorithm : the superior half of the Geneva commune, the Carouge commune and the left half of the Plan-les-Ouates commune, but more can be seen, looking more closely.

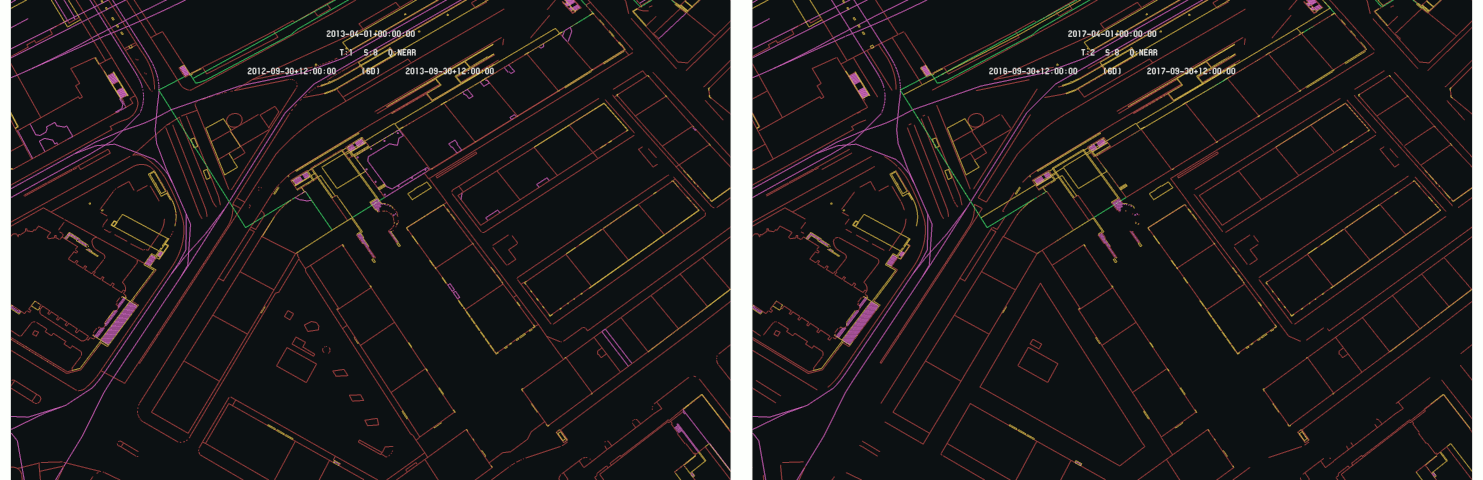
These zones have been subjected to correction during the time interval separating the two models. These corrections mainly comes from the FINELTRA [1] adjustment used to ensure conversion between the old Swiss coordinates system MN03 and the MN95 current standard. As these corrections operate on each coordinate, the whole area is then modified of the order of a few centimeters. In these condition, the whole area is then highlighted by the difference detection algorithm as illustrated by the following image on the Carouge commune :

Closer view of the Carouge 2019-04 and 2017-04 differences with 2019-04 as primary

On this closer view, one can see that almost all the primitive of this specific commune have been corrected. Some exceptions remain. It is the case of the train tracks for example, that appear as static between the two models. Looking more closely, one can also observe that some primitive were not affected by the correction.

Looking at the areas that have not been corrected through the FINELTRA triangular model, one can see that a lot of modification appear. For example, the following two images gives the differences of the Geneva historical part and the Verbois dam :

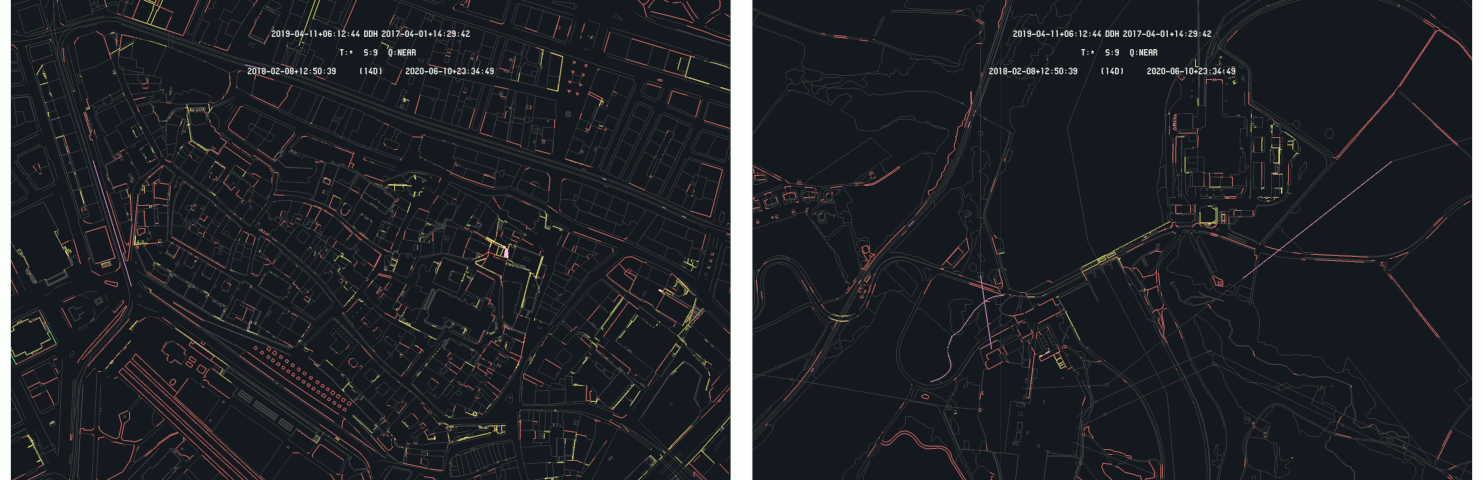
Closer view of the Historical city (left) and Verbois dam (right) 2019-04 and 2017-04 differences with 2019-04 as primary

One can see that, despite very few elements truly changed, a lot of primitives are highlighted as differences. This can be explained by a constant work of correction based on in-situ measurement. Some other factors can also explain these large amount of differences such as scripts used to correct the data to bring them in the expected Swiss standards.

In such context, detected real changes of the territory is made much more complicated, as large amounts of detected differences are due to corrections of the model itself, without underlying true modification on the territory. Nevertheless, differences that corresponds to a true territory modification can be found. The following images show an example on the Chemin du Signal in Bernex :

Differences on Chemin du Signal in Bernex with 2019-04 (left) and 2017-04 (right) as primary

These differences can be detected by the user on the difference model as they appear more clearly due to an accumulation of highlighted primitives. Indeed, in case of simple correction, the highlighted primitive appear more isolated. The following images give the formal situation for the two times :

Situation of Chemin du Signal in Bernex in 2019-04 (left) and 2017-04 (right)

On this example, one can see that, with both time as primary, the territory evolution can be seen by the user as the highlighted primitives are more consistent. Nevertheless, territory changes are more difficult to list in such a case than in the previous short-term analysis. The following images give two example of visible territory changes in the difference model :

La Gradelle (left) and Puplinge (right) 2019-04 and 2017-04 differences with 2019-04 as primary

On the previous left image, a clear block of buildings can be seen as more highlighted than the rest of the difference model and correspond to new building. On the right of this block, a smaller one can also be seen that also corresponds to new buildings. On the right images, a clear block of new buildings is also visible, as more highlighted. In such a case, the user has more effort to perform in order to detect the differences that correspond to true changes in the territory, the differences model showing the land register modification in the first place rather than of the proper territory evolution.

Considering the 2013-04 model, similar observations apply with stronger effect due to the larger temporal gap. The difference models are dominated by correction made to the model rather than proper territory changes. Comparing the 2017-04 and 2013-04 lead to even more difficult detection of these true modification, as the correction are widely dominating the difference models.

The case of the 2009-10 model is made even worse by its coordinates system, as it is expressed in the old MN03 coordinates system. This model is made very difficult to compare with the three others, expressed in the MN95 frame, as all its primitives are highlighted in difference models due to the conversion performed between the MN03 and MN95 frames. Comparing the 2009-10 model with the 2013-04 lead to no primitive detected as identity, leaving only differences.

Conclusion : Second Phase

Two cases have been addressed in this phase showing each specific interesting application of the difference detection applied on land register data through the INTERLIS format. Indeed, short and long term differences emphasize two different points of view according to the analysis of the land register and its evolution in time.

In the first place, the short term application clearly showed how difference detection and their representation opens a new point of view on the evolution of the land register as it allows focusing on clear and well identified modifications. As the compared models are close in time, one is able to produced differences models allowing to clearly see, modification by modification, what happened between the two compare situations, allowing focusing on each evolution to fully understand the modification.

It follows that this short-term difference detection can provide a useful approach for the user of the land register that are more interested in the evolution of the model rather than in the model itself. The difference models can provide users a clear a simple view on what to search and to analyze to understand the evolution of such complex models. In some way, the differences on land register models can be seen as an additional layer proposed to the user to allow him to reach information that are not easy to extract from the models themselves.

The case of Geneva, illustrating the long-term difference detection case, showed another interesting point of view. In the first place, one has to understand that land register models are complex and living models, not only affected by the transcription of the real-world situation across the time.

Indeed, on the Geneva models, a large amount of differences is detected even on a relative short period of time (two years). In addition to the regular updates, following the territory evolution, a large amount of corrections is made to keep the model in the correct reference frame. The Swiss federal system can also add complexity, as all Cantons have to align themselves on a common set of expectations.

In such a case, the difference detection turned out to be an interesting tool to understand and follows the corrections made to the model in addition to the regular updates. On the Geneva case, we illustrated that, by detecting it in the difference model, the correction on the coordinates frame on large pieces of the territory. This shows how the difference detection can be seen as a service that can help to keep track of the life of the model by detecting and checking these type of modifications.

As a result, difference detection can be a tool for the user of the land register but can also be a tool for the land register authorities themselves. The difference models can be used to check and audit the evolution of the models, helping the required follow-up on the applied correction and updates.

Third Phase : Point-Based Models

In this third and last phase, the developed algorithm for difference detection on vector models is tested on point-based ones. As mentioned in the introduction, the platform was already implementing logical operators allowing comparing point-based models across time. As illustrated in the introduction, only the AND operator allowed emphasizing differences, but rendering them as missing part of the composite models. It was then difficult for the user to determine and analyze those differences.

The goal of this last phase is to determine in which extend the developed algorithm is able to improve the initial results of point-based logical operators and how it can be adapted to provide better detection of differences.

Selected Resources and Models

Point-Based Models : LIDAR

Smaller data-sets are considered as point-based models are usually much larger. The city of Geneva is chosen as an example. Four identical chunks of LIDAR data are considered covering the railway station and its surroundings. The four models correspond to the digitization campaigns of 2005, 2009, 2013 and 2017. The data are converted from LAS to UV3 and brought to WGS84 using the EGM96-5 geoid model. The following images give an overview of the selected models :

Point-based data-sets : Geneva LIDAR of 2005 (left) and 2009 (right) - Data : SITG

The following table gives a summary of the models sizes and primitive count :

Model	Size (UV3)	Primitive Count
Geneva 2005	663.2 Mio	24.8 M-Points
Geneva 2009	1.2 Gio	46.7 M-Points
Geneva 2013	3.9 Gio	4.2 G-Points
Geneva 2017	7.0 Gio	7.5 G-Points

The color of the models corresponds to the point classification. In addition, the models have a density that considerably increases with time, from 1 points/m^2 (2005) to 25 points/m^2 (2017). This disparity of density is considered as part of the sampling disparity, leading to a set of data very interesting to analyze and benchmark the difference detection algorithm.

Models : Statistical Analysis

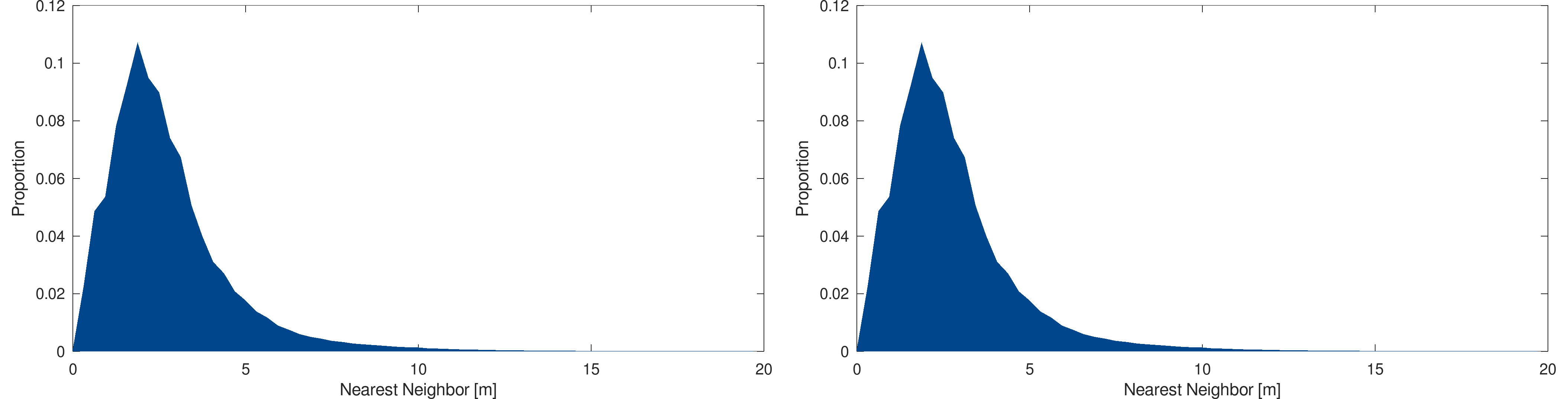
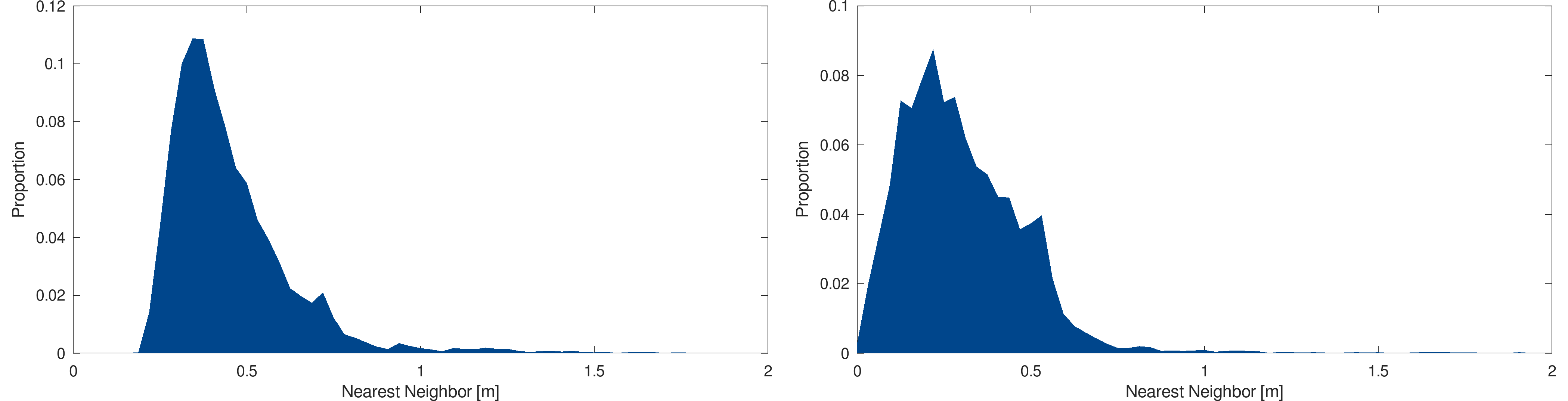
As for line and triangle-based models, a statistical analysis of the point-based models is performed. The analysis consists in computing an approximation of the nearest neighbor distance distribution of points. The following figure shows the distribution of the 2005 and 2009 models :

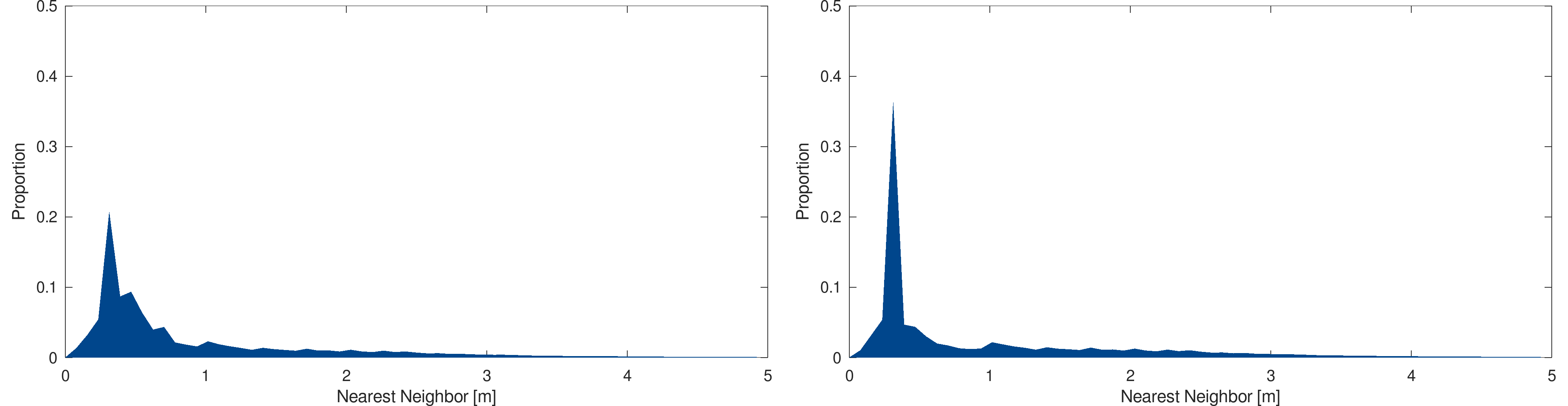
Statistical analysis : Nearest neighbor distribution approximation of the 2005 (left) and 2009 (right) models

and the following figure shows the results for the 2013 and 2017 models :

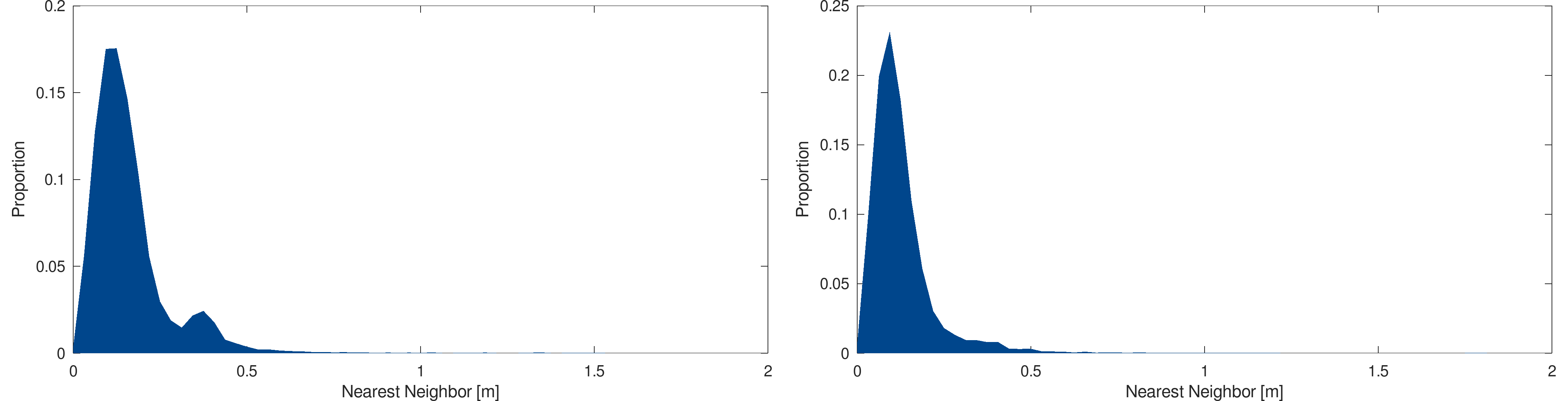
Statistical analysis : Nearest neighbor distribution approximation of the 2013 (left) and 2017 (right) models

The nearest neighbor distribution tends to go toward zeros with the year of acquisition, showing that modern models are significantly denser that the older ones, making these models interesting for the difference detection algorithm analysis.

Differences Detection Algorithm : Direct Application on Point-Based Models

In order to determine the performances of the difference detection algorithm on the selected point-based models, the algorithm is simply applied without any adaptation on the data-sets and the results are analyzed. The following images give an overview of the obtained results comparing the 2005 and 2009 models :

Application of the difference detection algorithm on point-based models : Geneva model of 2005 and 2009 with 2005 as primary (left) and inversely (right) - Data SITG

One can see that the obtained results are very similar to the results obtained with the previously implemented XOR logical operator. The only differences is that the identical points are shown (in dark gray) along with the highlighted points (showing the differences). The same conclusion applies : the obtained composite model is difficult to read as it is dominated by sampling disparities. One can, by carefully looking at the model, ending up detecting large modifications by searching for highlighted points accumulation. In addition, taking one model or the other as primary for the algorithm does not really help as shown on the images above. The same conclusion applies even when the two compared models comes with a similar point density as the 2013 and 2017 models :

Application of the difference detection algorithm on point-based models : Geneva model of 2013 and 2017 with 2013 as primary (left) and inversely (right) - Data SITG

One can nevertheless observe that choosing the less dense model as primary leads to results a bit more clear for difference detection, but remaining very hard to interpret for a user, and much more for automated processes.

In addition, the performances of the algorithm are very poor as point-based models are much denser in terms of primitives than line or triangle-based models. These reasons lead to the conclusion that the algorithm can not be directly used for point-based models and need a more specific approach.

Differences Detection Algorithm : Adaptation for Point-Based Models

In order to adapt the difference detection algorithm for point-based models, two aspects have to be addressed : the efficiency of the detection and the reduction of the sampling disparities over-representation, which are both server-side operations.

The problem of efficiency can be solved quite easily if the adaptation of the difference detection algorithm goes in the direction of logical operators, for which an efficient methodology is already implemented. Solving the sampling disparity over-representation is more complicated.

The adopted solution is inspired from a simple observation : the less deep (density of cells) the queries are, the clearer the obtained representation is. This can be illustrated by the following images showing the 2005 model compared with the 2009 one with depth equal to 7, 6 and 5, from left to right :

Example of decreasing query depth on the comparison of 2005 and 2009 models - Data SITG

This is expected, as the sampling disparities can only appear at scales corresponding to the nearest neighbor distribution. Nevertheless, as the depth is decreased, the models become less and less dense. The increase of difference readability is then compensated by the lack of density, making the structures more difficult to identify, and then, their subsequent modifications. The goal of the algorithm adaptation is to keep both readability and density.

To achieve this goal, the implementation of the previous XOR operator is considered as a base, mostly for its efficiency. As the XOR simply detects if a cell of the space-time discretization at a given time is in a different state as its counterpart at another time, it can be modulated to introduce a scale delay mechanism that only applies detection on low-valued scales, broadcasting their results to their daughter cells. This allows to preserve the density and to perform the detection only on sufficiently shallow scales to avoid sampling disparities to become dominant.

The question is how to operate the scale delay according to the scale itself. Indeed, with large points of view, the delay is not necessary as the model is viewed from far away. The necessity of the scale delay appears as the point of view is reduced, and, the more it is reduced, the larger the scale delay needs to be. A scale-attached delay is then defined to associate a specific value for each depth.

Results and Experiments

The adaptation of the difference detection algorithm for point-based models is analyzed using the selected data-sets. An overview of its result is presented before a more formal analysis is made using difference detection made on line-based official land register data to be compared with the differences on point-based models.

Differences Detection : Overview

Considering the two first models, from 2005 and 2009 campaigns, the following images shows the results of the initial version of the difference detection algorithm (similar to XOR operator) and its adapted version implementing the scale delay :

Differences detection on 2005 and 2009 models with 2005 as primary - Left : without scale delay - Right : with scale delay - Data SITG

One can see how scale delay is able to drastically reduce the effect of sampling disparities while comparing two point-based models. The effect is more obvious as the 2009 model is set as primary for difference detection :

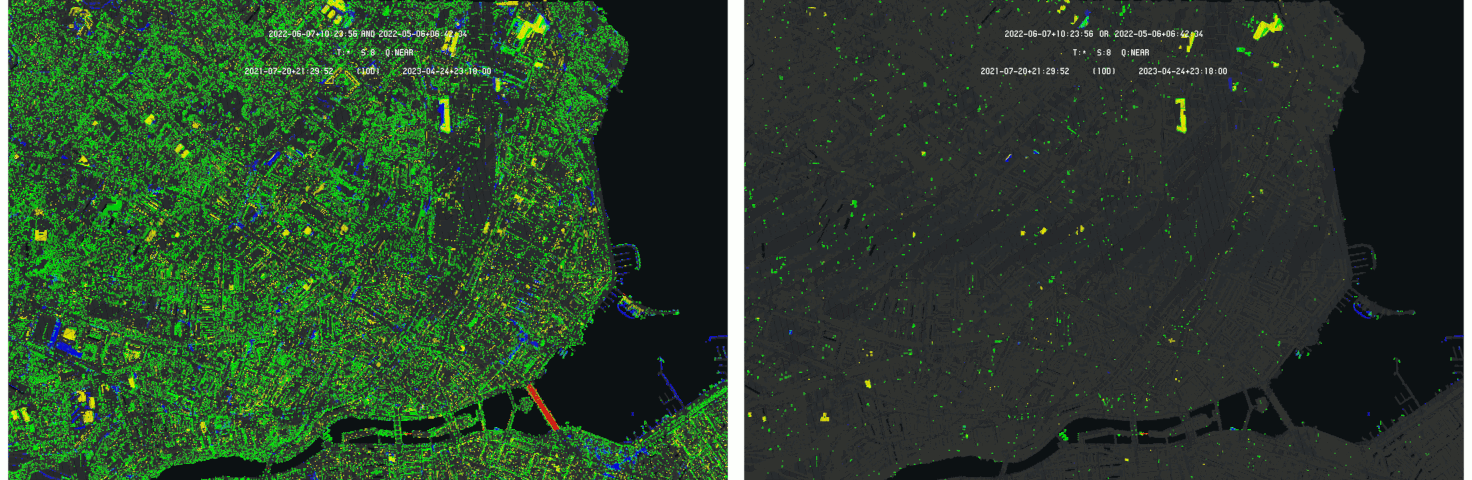
Differences detection on 2005 and 2009 models with 2009 as primary - Left : without scale delay - Right : with scale delay - Data SITG

This improvement gets more clear as the point of view is reduced. The following image shows the initial algorithm and the scale delay algorithm on a specific area of the city with 2005 as primary model :

Differences detection on 2005 and 2009 models with 2005 as primary - Left : without scale delay - Right : with scale delay - Data SITG

By inverting the model roles and making the 2009 model primary for difference detection lead to similar results :

Differences detection on 2005 and 2009 models with 2009 as primary - Left : without scale delay - Right : with scale delay - Data SITG

Considering the denser models of 2013 and 2017 campaigns, the results of the scale delay introduction also lead to a better understanding of the differences as shown on the following images :

Differences detection on 2013 and 2017 models with scale delay - Left : 2013 as primary - Right : 2017 as primary - Data SITG

Nevertheless, one can see that scale delay is not able to get rid entirely of sampling disparities. The right image above, comparing the 2017 model to the 2013 one, shows sampling disparities being highlighted as differences on the wall of the building in the background. This does not affect too much the user readability, but still make the model a bit more complicated to understand.

In addition, the models play an important role in the way differences can be detected through classic approach. For example, focusing on a specific building, the obtained highlighted differences :

Differences detection on 2013 and 2017 models with scale delay with 2013 (left) and 2017 (right) as primary - Data SITG

could lead the user to consider the building wall as a difference. Looking at the formal situation in both 2013 and 2017 models :

Structural situation in 2013 (left) and 2017 (right) - Data SITG

One can see that the detected difference comes from the missing wall on the 2013, and not from a formal evolution of the building. This example illustrates that sampling disparity is not the only factor that could reduce the readability of the model for the user.

Differences Detection : Comparison with Land Register Differences

As the algorithm is already tested for land register models, one can use its results on these data in order to put them into perspective of the detected differences on point cloud. As the methodology is not the same for vector-based and point-based models, it is interesting to see the coherence and deviations of both approaches.

One important thing to underline, is that difference detection in land register model does not detect changes in the environment directly, but detects the revision of the land register itself, as discussed in the previous phase. Of course, land register models evolve with environment, but come also with a large amount of modifications that only represent corrections of the model and not formal changes in the environment. This reason reinforces the interest to but point-based model difference detection with the land register models ones.

In the previous phase, the land register models of Geneva were selected to be the closest to the LIDAR campaigns. It follows, that these models can be directly used here, as each corresponding to the compared point-based model of this phase.

As a first example, the following case is studied : Rue de Bourgogne and Rue de Lyon. In this case, looking at the following images giving the situation in 2013-04 and 2017-04 through the LIDAR models, that an industrial building was partially demolished.

Structural situation in 2013 (left) and 2017 (right) - Data SITG

The following images show the differences computed on both point-based and line-based models :

Difference models between 2013 and 2017 of LIDAR (left) and INTERLIS (right), with 2013 as primary - Data SITG

One can clearly see that the difference detection on the LIDAR models correctly emphasized a true structural difference between the two times. The situation is much less clear on the land register model. Indeed, as the time separating the two models is quite high, four years in such a case, a large mount of corrections dominates the difference model, leading to a difficult interpretation of the building situation change. The following images give the situation of the land register model in 2013 and 2017 that lead to the difference model above :

Land register situation in 2013 (left) and 2017 (right) - Data SITG

Looking at the land register models, one can also see that such large scale modification of the building situation does not appear clearly. Indeed, it takes some effort to detect minor changes on the two models, without leading to a clear indication of the modification. This shows how the LIDAR and its differences can help to detect and analyze differences in complement to the land register itself.

Considering the second example, Avenue de France and Avenue Blanc, the following images give the structural situation of the two times as capture by the LIDAR campaigns :

Structural situation in 2013 (left) and 2017 (right) - Data SITG

One can clearly see the destruction of the two 2013 buildings replaced by a parking lot in 2017. The detected differences on the LIDAR and land register models are presented on the following images :

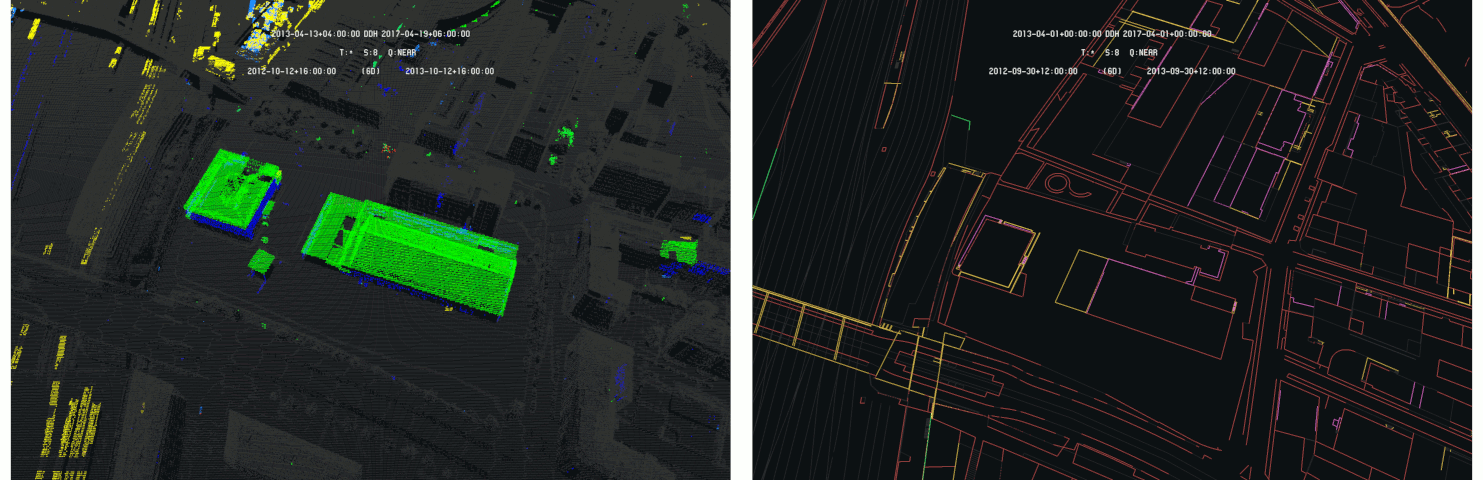
Difference models between 2013 and 2017 of LIDAR (left) and INTERLIS (right), with 2013 as primary - Data SITG

Again, despite the differences are clearly and correctly highlighted on the LIDAR differences model, the situation remains unclear on the differences model of the land register. Again, one can observe that the land register was highly corrected between the two dates, leading to difficulties to understand the modification and its nature. Looking at the land register respective models :

Land register situation in 2013 (left) and 2017 (right) - Data SITG

the modification appears a bit more clearly. One can clearly see the disappearance of the two 2013 buildings in the land register replaced by a big empty area. Again, the difference detection on LIDAR seems clearly more relevant to detect and analyze structural differences than the land register itself.

An interesting example is provided by the situation just east of the Basilique Notre-Dame. The two situations as captured by the LIDAR campaigns are presented on the following images :

Structural situation in 2013 (left) and 2017 (right) - Data SITG

One can observe two structure mounted on top of two buildings roof in the 2013 situation. These structures are used to ease the work that has to be performed on the roofs. These structures are no more present in the 2017 situation. The following images give the difference detection models for the LIDAR and land register :

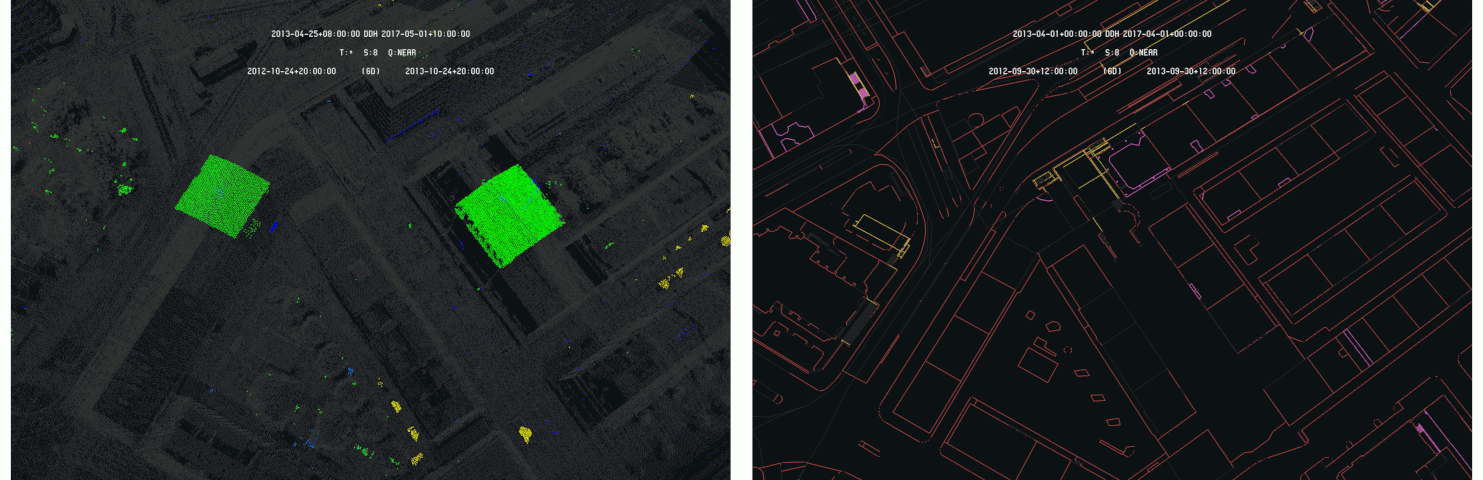
Difference models between 2013 and 2017 of LIDAR (left) and INTERLIS (right), with 2013 as primary - Data SITG

In such a case, as the structural modification between 2013 and 2017 occurs on top of the buildings, their footprints is not affected and the differences have no chance to appear in the land register models, even looking at them individually as in the following images :

Land register situation in 2013 (left) and 2017 (right) - Data SITG

This is another example where the LIDAR difference detection lead to more and clearer information on the structural modification that appear on Geneva between the two times.

Conclusion : Third Phase

The main element of this third phase conclusion is that difference detection on point-based models is less straightforward than for other models. Indeed, applied naively, the algorithm is dominated by the sampling disparities of the compared models. This illustrate that point-based models, being a close mirror of the true territory state, have a large information density that is more difficult to reach, especially from their evolution point of view.

Nevertheless, we showed that the algorithm can be adapted, with relatively simple adjustments, to perform well on point-based models difference detection problem. The implemented algorithm is able to track and represent the differences appearing between the models in a useful and comprehensive way for users. The proposed example showed that the differences models are able to guide the user toward interesting structural changes in the territory, with a clear view of the third dimension.

Of course, the highlighted differences in point-based models are more complex and required a trained user that is able to interpret correctly the detail of the highlighted part of the model. The trees are a good example. As the tree re-grow each year, they will always appear as a differences in the compared models. A user only interested in building changes has to be aware of that and be able to separate the relevant differences from the others.

Following the comparison between LIDAR and land register (INTERLIS) differences models, a very surprising conclusion appear. In the first place, one could stand that land register is the proper way of detected changes that can be then analyzed more in detail in point-based differences models. In turns out that to opposite is true. Several reason explain this surprising situation.

In the first place, LIDAR are available only with large temporal gaps between them, at least two/three years. This allows the land register models to be filled with large amount of updates and correction, leading the differences model on this temporal gap to be filled with much more than structural modification. In addition, the LIDAR models come with the third dimension where the land register models are flat. The third dimension comes with large amount of differences that can not be seen in the land register.

To some extend, the land register, and its evolution, is the reflect of the way the territory is surveyed, not the reflect of the formal territory evolution. In the opposite, as LIDAR models are a structural snapshot of a territory situation, the analyze of their differences across the time lead to a better tracking of the formal modification of the real world.

Conclusion

First Phase

In the first phase, the difference detection algorithm was implemented for vector models and tested using synthetic differences on selected models. The results showed the interest of the obtained differences models to emphasize evolution of models from both user and process points of view. It was demonstrated that the information between models exists and can be extracted and represented in a relevant way for both users and processes.

Second Phase

In the second phase, the difference detection algorithm was tested on the Swiss land register models on which the results obtained during the first phase were confirmed. The differences models are able to provide both user and process a clear and understandable view of the modification brought to the models.

In addition, through the short and long-term perspectives, it was possible to demonstrate how the difference detection algorithm is able to provide different points of view on the model evolution. From a short-term perspective, the differences models are able to provide a clear and individual view of the modification while the long-term perspective allows to see the large scale evolution and transformation of the models. It follows that the difference models can be used as a tool for various actors using or working with the land register models.

Third Phase

In the third phase, the difference detection algorithm, developed on vector models, was applied on point-based models, showing that a direct application on these models lead to the same issue as the logical operators : the differences models are dominated by sampling disparities, making them complicated to read. The solution of scale delay brought to the algorithm allowed to produce much clearer differences models for point-based data, allowing to generalize the difference detection on any models.

In addition to these results, the comparison of difference models on land register and on their corresponding LIDAR point-based models showed an interesting result : for structural changes, the point-based models lead to much more interesting results through the highlighted differences. Indeed, as land register models, considered long term perspective, are dominated by a large amount of corrections and adjustments in addition to territory evolution updates, making the structural changes not easy to detect and understand. The differences models are more clear with point-based models form this point of view.

In addition, as point-based models, such as LIDAR, come with the third dimension, a large amount of structural differences can only be seen through such data as many structural changes are made along the third dimension. It then follows that difference detection applied to point-based models offers a very interesting point of view for the survey of territory structural changes.

Synthesis

As a synthesis, it is clear that models are carrying a large amount of richness themselves, that is already a challenge to exploit, but it is also clear that a large amount of information can be found between the versions of the models. The difference detection algorithm brings a first tool that demonstrate the ability to reach and start to exploit these informations.

More than the content of the models itself, the understanding of the evolution of this content is a major topic especially in the field of geodata as they represent, transcript, the evolution of the surveyed territory. It then appears clear that being able to reach and exploit the information contained in-between the models is a major advantage as it allows understanding what are these models, that is four dimensional objects.

Perspectives

Many perspectives are opened following the implementation and analysis of the difference detection. Several perspectives, mostly technical, are presented here as a final section.

In the first place, as raster are entering the set of data that can be injected in the platform, evolution of the difference detection could be applied to the platform, taking advantage of the evolution of machine learning. The possibility of detected differences in images could lead to very interesting perspective through the data communication features of the platform.

Another perspective could be to allow the platform to separate the data into formal layers, the separation being only currently ensure by type and times. Splitting data into layers would allow applying difference detection in a much more controlled manner, leading to difference models focused on very specific elements of the model temporal evolution.

The addition of layer could also be the starting point to the notion of data convolution micro language. Currently, data communication and difference detection only apply through the specification of two different and parallel navigation time. The users, or processes, have to specify each of the two time position in order to obtain the mixed of differences models they need.

An interesting evolution would be to replace these two navigation time by a small and simple micro language allowing the user to compare more than two times in a more complex manner. This could also benefit from data separation through layer. Such micro language could allow to compare two, three or more models, or layers, and would also open the access the mixed models of differences models such as comparing the difference detection between point-based and vector-based models, which would then be a comparison of a comparison.

Reproduction Resources

To reproduce the presented experiments, the STDL 4D framework has to be used and can be found here :

• STDL 4D framework (eratosthene-suite), STDL

You can follow the instructions on the README to both compile and use the framework.

Only part of the considered datasets are publicly available. For the OpenStreetMap datasets, you can download them from the following source :

• Shapefile layers, OpenStreetMap

For the Swiss 3D buildings model, you can contact swisstopo :

• Shapefile 3D buildings, swisstopo

For the land register datasets of Geneva and Thurgau, you can contact the SITG and the Thurgau Kanton :

• INTERLIS land register, Thurgau Kanton

• INTERLIS land register, SITG (Geneva)

The point-based models of Geneva can be downloaded from the SITG online extractor :

• LAS MNS, SITG (Geneva)

To extract and convert the data from planimetric shapefiles, the following code is used :

• Shapefile CSV export to UV3(csv-wkt-to-uv3), STDL

where the README gives all the information needed. In case of shapefile containing 3D models, please ask the STDL for advice and tools.

To extract and convert the data from INTERLIS and LAS, the following codes are used :

• INTERLIS to UV3 (dalai-suite), STDL/EPFL

• LAS to UV3 (dalai-suite), STDL/EPFL

where the README gives all the information needed.

For the 3D geographical coordinates conversion and heights restoration, we used two STDL internal tools. You can contact the STDL to obtain the tools and support in this direction :

• ptolemee-suite : 3D coordinate conversion tool (EPSG:2056 to WGS84)

• height-from-geotiff : Restoring geographical heights using topographic GeoTIFF (SRTM)

You can contact STDL for any question regarding the reproduction of the presented results.

Auxiliary Developments & Corrections

In addition to the main developments made, some additional scripts and other corrections have been made to solve auxiliary problems or to improve the code according to the developed features during this task. The auxiliary developments are summarized here :

• Correction of socket read function to improve server-client connectivity.

• Creation of scripts that allows to insert synthetic modifications (random displacements on the vertex coordinates) on UV3 models.

• Creation of a script to convert CSV export from shapefile to UV3 format. The script code is available here.

• Adding temporary addresses (space-time index) exportation in platform 3D interface.

• Correction of the cell enumeration process in platform 3D interface (wrong depth limit implementation).

• Creation of a script allowing segmenting UV3 model according to geographical bounding box.

• Creation of C codes to perform statistical analysis of the point, line and triangle-based models : computation of edge size and nearest neighbor distributions.

• Creation of a C code allowing enumerating non-empty cell index over the Switzerland models injected in the platform.

• Creation of a C code allowing to automate the difference detection based on an index list and by searching in the data queried from the platform.

• Developments of various scripts for plots and figures creations.

References

[1] REFRAME, SwissTopo, https://www.swisstopo.admin.ch/de/karten-daten-online/calculation-services.html